Chapter: 11th Physics : UNIT 5 : Motion of System of Particles and Rigid Bodies
Torque and Angular Momentum - Final Derivation
Torque and Angular Momentum
We have the expression for magnitude of angular momentum of a rigid body as, L = I ω . The expression for magnitude of torque on a rigid body is, τ = I α
We can further write the expression for torque as,
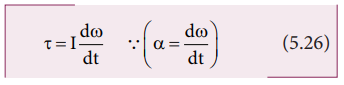
Where, ω is angular velocity and a is angular acceleration. We can also write equation 5.26 as,

The above expression says that an external torque on a rigid body fixed to an axis produces rate of change of angular momentum in the body about that axis.
This is the Newton’s second law in rotational motion as it is in the form of F = dp/dt which holds good for translational motion.
Conservation of angular momentum:
From the above expression we could conclude that in the absence of external torque, the angular momentum of the rigid body or system of particles is conserved.
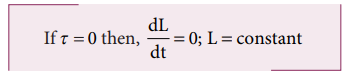
The above expression is known as law of conservation of angular momentum. We will learn about this law further in section 5.5.
Related Topics