Chapter: 11th Physics : UNIT 5 : Motion of System of Particles and Rigid Bodies
Angular Momentum and Angular Velocity
Angular Momentum and Angular Velocity
Let us consider a rigid body rotating about a fixed axis. A point mass m in the body will execute a circular motion about the fixed axis as shown in Figure 5.12.
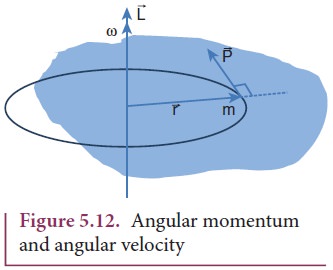
The point mass m is at a distance r from the axis of rotation. Its linear momentum at any instant is tangential to the circular path. Then the angular momentum 
is perpendicular to 
and 
. Hence, it is directed along the axis of rotation. The angle θ between and in this case is 90o. The magnitude of the angular momentum L could be written as,
L = rmv sin90o = rmv
where, v is the linear velocity. The relation between linear velocity v and angular velocity ω in a circular motion is, v = r ω. Hence,
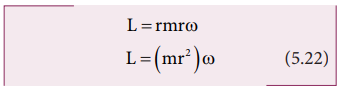
The directions of L and ω are along the axis of rotation. The above expression can be written in the vector notation as,
As discussed earlier, the term mr2 in equations 5.22 and 5.23 is called moment of inertia (I) of the point mass. A rigid body is made up of many such point masses. Hence, the moment of inertia of a rigid body is the sum of moments of inertia of all such individual point masses that constitute the body ( I = ∑mi ri 2 ). Hence, the angular momentum of the rigid body can be written as,
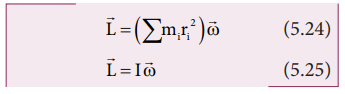
The study about moment of inertia (I) is reserved for Section 5.4.
Related Topics