Chapter: 11th Physics : UNIT 5 : Motion of System of Particles and Rigid Bodies
Moment of Inertia of a Uniform Ring
Moment of Inertia of a Uniform Ring
Let us consider a uniform ring of mass M and radius R. To find the moment of inertia of the ring about an axis passing through its center and perpendicular to the plane, let us take an infinitesimally small mass (dm) of length (dx) of the ring. This (dm) is located at a distance R, which is the radius of the ring from the axis as shown in Figure 5.22.
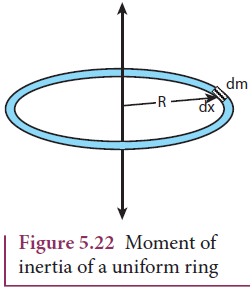
The moment of inertia (dI) of this small mass (dm) is,
dI = (dm)R2
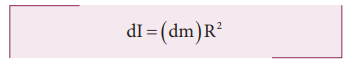
The length of the ring is its circumference ( 2πR). As the mass is uniformly distributed, the mass per unit length (λ) is,
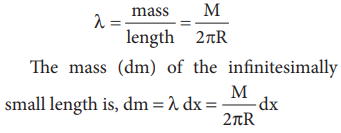
Now, the moment of inertia (I) of the entire ring is,
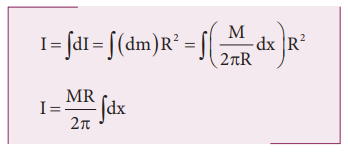
To cover the entire length of the ring, the limits of integration are taken from 0 to 2πR.
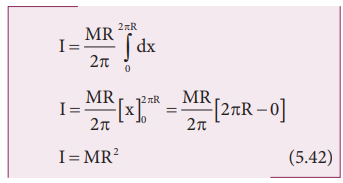
Related Topics