Chapter: 11th Physics : UNIT 5 : Motion of System of Particles and Rigid Bodies
Moment of Inertia of a Uniform Rod
Moment of Inertia of a Uniform Rod
Let us consider a uniform rod of mass (M) and length (l) as shown in Figure 5.21. Let us find an expression for moment of inertia of this rod about an axis that passes through the center of mass and perpendicular to
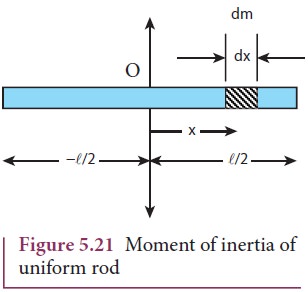
First an origin is to be fixed for the coordinate system so that it coincides with the center of mass, which is also the geometric center of the rod. The rod is now along the x axis. We take an infinitesimally small mass (dm) at a distance (x) from the origin. The moment of inertia (dI) of this mass (dm) about the axis is,
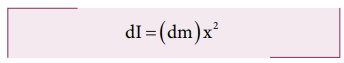
As the mass is uniformly distributed, the mass per unit length (λ) of the rod is, λ = M/l
The (dm) mass of the infinitesimally small length as, dm = λdx = M/l dx
The moment of inertia (I) of the entire rod can be found by integrating dI,
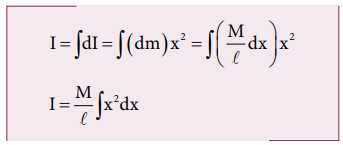
As the mass is distributed on either side of the origin, the limits for integration are taken from − l/ 2 to l/ 2.
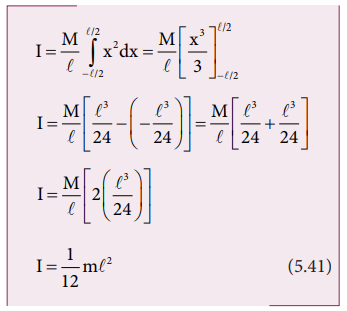
Solved Example Problems for Moment of Inertia of a Uniform Rod
Example 5.14
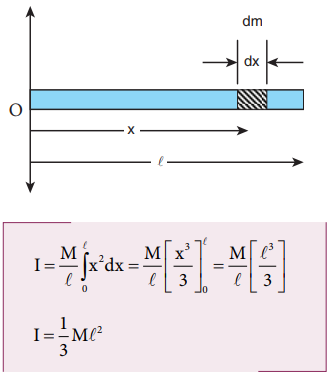
Find the moment of inertia of a uniform rod about an axis which is perpendicular to the rod and touches any one end of the rod.
Solution
The concepts to form the integrand to find the moment of inertia could be borrowed from the earlier derivation. Now, the origin is fixed to the left end of the rod and the limits are to be taken from 0 to ℓ.
Related Topics