Chapter: 11th Physics : UNIT 5 : Motion of System of Particles and Rigid Bodies
Torque about an Axis
Torque about an Axis
In the earlier sections, we have dealt with the torque about a point. In this section we will deal with the torque about an axis. Let us consider a rigid body capable of rotating about an axis AB as shown in Figure 5.8. Let the force F act at a point P on the rigid body. The force F may not be on the plane ABP. We can take the origin O at any random point on the axis AB.

Th e torque of the force ![]() about O is,
about O is, ![]() =
= ![]() x
x![]() . Th e component of the torque along the axis is the torque of
. Th e component of the torque along the axis is the torque of ![]() about the axis. To find it, we should first find the vector
about the axis. To find it, we should first find the vector ![]() = |
= |![]() x
x![]() | and then find the angle φ between
| and then find the angle φ between ![]() and AB. (Remember here,
and AB. (Remember here, ![]() is not on the plane ABP). Th e torque about AB is the parallel component of the torque along AB, which is |
is not on the plane ABP). Th e torque about AB is the parallel component of the torque along AB, which is | ![]() x
x![]() | cos φ. And the torque perpendicular to the axis AB is |
| cos φ. And the torque perpendicular to the axis AB is | ![]() x
x![]() | sin φ|.
| sin φ|.
The torque about the axis will rotate the object about it and the torque perpendicular to the axis will turn the axis of rotation. When both exist simultaneously on a rigid body, the body will have a precession. One can witness the precessional motion in a spinning top when it is about to come to rest as shown in Figure 5.9.
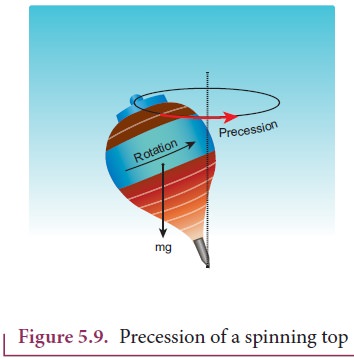
Study of precession is beyond the scope of the higher secondary physics course. Hence, it is assumed that there are constraints to cancel the effect of the perpendicular components of the torques, so that the fixed position of the axis is maintained. Therefore, perpendicular components of the torque need not be taken into account.
Hereafter, for the calculation of torques on rigid bodies we will:
a. Consider only those forces that lie on planes perpendicular to the axis (and do not intersect the axis).
b. Consider position vectors which are perpendicular to the axis.
The torque of a force about an axis is independent of the choice of the origin as long as it is chosen on that axis itself. This can be shown as below.
Let O be the origin on the axis AB, which is the rotational axis of a rigid body. F is the force acting at the point P. Now, choose another point O’ anywhere on the axis as shown in Figure 5.10.
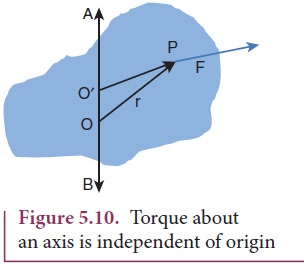
The torque of F about O’ is,

Solved Example Problems for Torque about an Axis
Example 5.10
Three mutually perpendicular beams AB, OC, GH are fixed to form a structure which is fixed to the ground firmly as shown in the Figure. One string is tied to the point C and its free end D is pulled with a force F. Find the magnitude and direction of the torque produced by the force,
i. about the points D, C, O and B
ii. about the axes CD, OC, AB and GH.
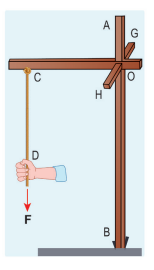
Solution

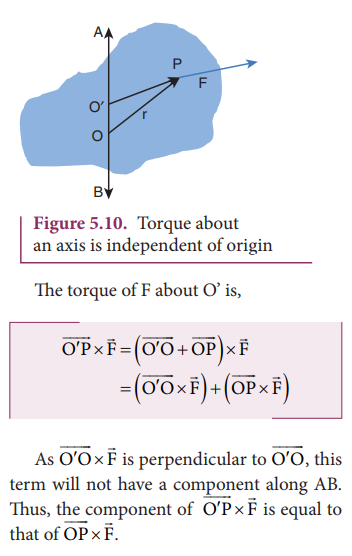
The torque of a force about an axis is independent of the choice of the origin as long as it is chosen on that axis itself. Th is can be shown as below.
Let O be the origin on the axis AB, which is the rotational axis of a rigid body. F is the force acting at the point P. Now, choose another point O’ anywhere on the axis as shown in Figure 5.10.
Related Topics