Chapter: 11th Physics : UNIT 5 : Motion of System of Particles and Rigid Bodies
Moment of Inertia of a Uniform Disc
Consider a disc of mass M and radius R.
Moment of Inertia of a Uniform Disc
Consider a disc of mass M and radius R. This disc is made up of many infinitesimally small rings as shown in Figure 5.23. Consider one such ring of mass (dm) and thickness (dr) and radius (r). The moment of inertia (dI ) of the small ring is,

The mass of the infinitesimally small ring is,
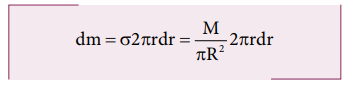
where, the term ( 2πr dr ) is the area of this elemental ring (2πr is the length and dr is the thickness). dm = 2M/R2 rdr

The moment of inertia (I) of the entire disc is,

Study Material, Lecturing Notes, Assignment, Reference, Wiki description explanation, brief detail
11th Physics : UNIT 5 : Motion of System of Particles and Rigid Bodies : Moment of Inertia of a Uniform Disc |
Related Topics
11th Physics : UNIT 5 : Motion of System of Particles and Rigid Bodies