Book Back Numerical Problems

Numerical Problems

1. A uniform disc of mass 100g has a diameter of 10 cm. Calculate the total energy of the disc when rolling along a horizontal table with a velocity of 20 cms-1. (take the surface of table as reference)

Answer

Mass of the disc m = 100 g = 0.1 kg.

Diameter of the disc d = 10 cm

Radius of the disc r = 5 cm = 0.05m

Rolling with a velocity v = 20 cms-1 = 0.20 ms-1

Total energy of the disc ETot = ?

ETot = Translational K.E. + rotational K.E.

Moment of inertia (M.I) of the disc about its own axis

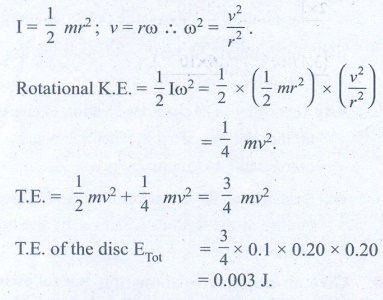
Ans: 0.1028 J

2. A particle of mass 5 units is moving with a uniform speed of v = 3√2 units in the XOY plane along the line y = x + 4. Find the magnitude of angular momentum.

Answer

Equation of line x - y + 4 = 0

Mass of particle = 5 units

Speed v - 3 √2 units

Distance of line from origin r = 

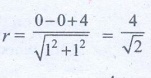
Angel momentum L = mvr = 5 × 3 √2 × 4/√2 = 60 units

Ans: 60 units

3. A fly wheel rotates with a uniform angular acceleration. If its angular velocity increases from 20π rad/s to 40π rad/s in 10 seconds. Find the number of rotations in that period.

Answer:

Initial Angular Velocity ω0 = 20π rad s-1

Final Angular velocity ω = 40 π rad s-1

time taken, t  = 10 s

No. of rotations / s = ?

= 150 rotations.

Ans: 150 rotations

4. A uniform rod of mass m and length l makes a constant angle θ with an axis of rotation which passes through one end of the rod. Find the moment of inertia about this axis.

Answer

θ - angle that rod makes with the axis (vertical)

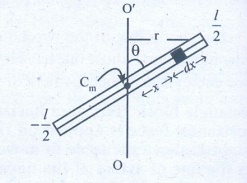
Linear mass density λ = m/l

Consider dx. the part of rod

Mass dx, the part of rod dm=λ.dx

dm= m/l dx. The M.I of the rod about OO'

I = ∫ r2 dm

Where is the perpendicular distance from the elementary mass dm.

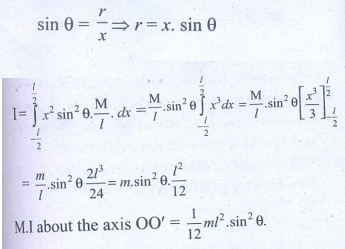
M.I about the axis OO' = 1/12 ml2.sin2 θ.

Ans: 1/12  Ml 2 sin2 θ

5. Two particles P and Q of mass 1kg and 3 kg respectively start moving towards each other from rest under mutual attraction. What is the velocity of their center of mass?

Answer

Mass of particle P m1 = 1 kg.

Mass of particle Q m2 = 3 kg

Velocity of particle P = velocity of particle Q

but in opposite direction.

velocity of center of mass vcm = ?

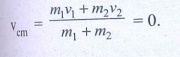
Ans: Zero

6. Find the moment of inertia of a hydrogen molecule about an axis passing through its center of mass and perpendicular to the inter-atomic axis. Given: mass of hydrogen atom 1.7 × 10-27 kg and inter atomic distance is equal to 4 × 10-10 m.

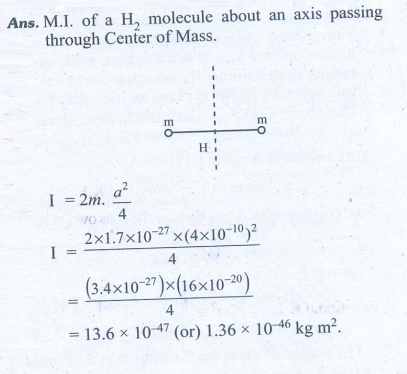
Ans: 1.36 × 10-46 kg m2

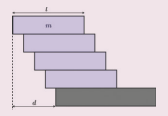
7. On the edge of a wall, we build a brick tower that only holds because of the bricks’ own weight. Our goal is to build a stable tower whose overhang d is greater than the length l of a single brick. What is the minimum number of bricks you need?

(Hint: Find the center of mass for each brick and add.)

8. The 747 boing plane is landing at a speed of 70m s-1. Before touching the ground, the wheels are not rotating. How long a skid mark do the wing wheels leave (assume their mass is 100 kg which is distributed uniformly, radius is 0.7 m, and the coefficient of friction with the ground is 0.5)?

Ans: 2.1 m