Chapter: 11th Physics : UNIT 5 : Motion of System of Particles and Rigid Bodies
Moment of Inertia
MOMENT OF INERTIA
In
the expressions for torque and angular momentum for rigid bodies (which are
considered as bulk objects), we have come across a term Σmi ri2. This quantity is
called moment of inertia (I) of the bulk object. For point mass mi
at a distance ri from the fixed axis, the moment of inertia is given
as, mi ri2.
Moment
of inertia for point mass,

Moment
of inertia for bulk object,

In
translational motion, mass is a measure of inertia; in the same way, for
rotational motion, moment of inertia is a measure of rotational inertia. The
unit of moment of inertia is, kg m2. Its dimension is M L2.
In general, mass is an invariable quantity of matter (except for motion
comparable to that of light). But, the moment of inertia of a body is not an
invariable quantity. It depends not only on the mass of the body, but also on
the way the mass is distributed around the axis of rotation.
To
find the moment of inertia of a uniformly distributed mass; we have to consider
an infinitesimally small mass (dm) as a point mass and take its position (r)
with respect to an axis. The moment of inertia of this point mass can now be
written as,

We
get the moment of inertia of the entire bulk object by integrating the above
expression.
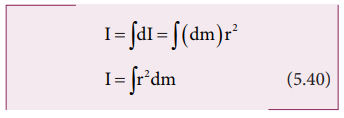
We
can use the above expression for determining the moment of inertia of some of
the common bulk objects of interest like rod, ring, disc, sphere etc.
Moment of Inertia of a Uniform Rod
Let
us consider a uniform rod of mass (M) and length (l) as shown in Figure 5.21. Let us find an expression for
moment of inertia of this rod about an axis that passes through the center of
mass and perpendicular to
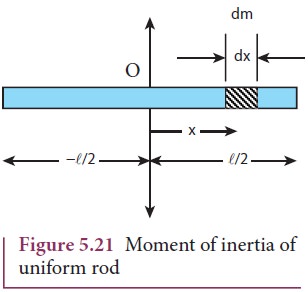
First an origin is to be fixed for the coordinate system so that it
coincides with the center of mass, which is also the geometric center of the
rod. The rod is now along the x axis. We take an infinitesimally small mass
(dm) at a distance (x) from the origin. The moment of inertia (dI) of this mass
(dm) about the axis is,
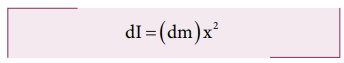
As
the mass is uniformly distributed, the mass per unit length (λ) of the rod is, λ = M/l
The
(dm) mass of the infinitesimally small length as, dm = λdx = M/l dx
The
moment of inertia (I) of the entire rod can be found by integrating dI,
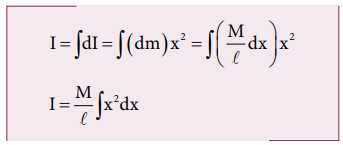
As
the mass is distributed on either side of the origin, the limits for
integration are taken from − l/
2 to l/ 2.
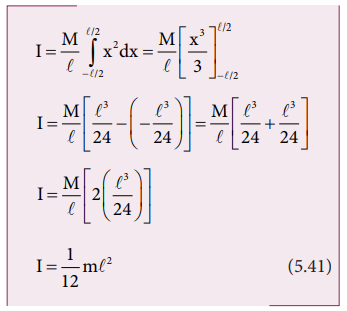
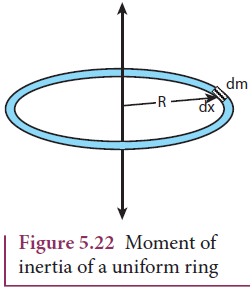
Moment of Inertia of a Uniform Ring
Let
us consider a uniform ring of mass M and radius R. To find the moment of
inertia of the ring about an axis passing through its center and perpendicular
to the plane, let us take an infinitesimally small mass (dm) of length (dx) of
the ring. This (dm) is located at a distance R, which is the radius of the ring
from the axis as shown in Figure 5.22.
The
moment of inertia (dI) of this small mass (dm) is,
dI = (dm)R2
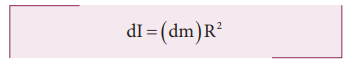
The
length of the ring is its circumference ( 2πR). As the mass is uniformly distributed,
the mass per unit length (λ) is,
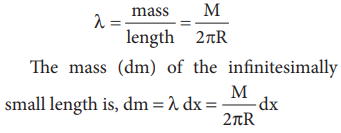
Now,
the moment of inertia (I) of the entire
ring is,
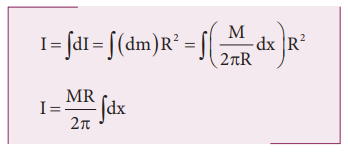
To
cover the entire length of the ring, the limits of integration are taken from 0
to 2πR.
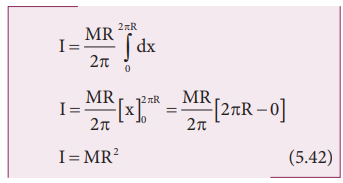
Moment of Inertia of a Uniform Disc
Consider
a disc of mass M and radius R. This disc is made up of many infinitesimally
small rings as shown in Figure 5.23. Consider one such ring of mass (dm) and
thickness (dr) and radius (r). The moment of inertia (dI ) of the small ring
is,

The
mass of the infinitesimally small ring is,
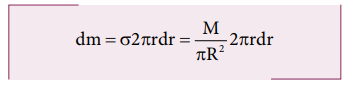
where,
the term ( 2πr dr ) is the area of this elemental ring
(2πr is the length and dr is the thickness). dm = 2M/R2 rdr

The
moment of inertia (I) of the entire disc is,

Radius of Gyration
For
bulk objects of regular shape with uniform mass distribution, the expression
for moment of inertia about an axis involves their total mass and geometrical
features like radius, length, breadth, which take care of the shape and the
size of the objects. But, we need an expression for the moment of inertia which
could take care of not only the mass, shape and size of objects, but also its
orientation to the axis of rotation. Such an expression should be general so
that it is applicable even for objects of irregular shape and non-uniform
distribution of mass. The general expression for moment of inertia is given as,
I=MK2 (5.44)
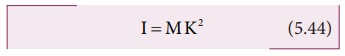
where,
M is the total mass of the object and K is called the radius of gyration,
The radius of gyration of an object
is the perpendicular distance from the axis of rotation to an equivalent point
mass, which would have the same mass as well as the same moment of inertia of
the object.
As
the radius of gyration is distance, its unit is m. Its dimension is L.
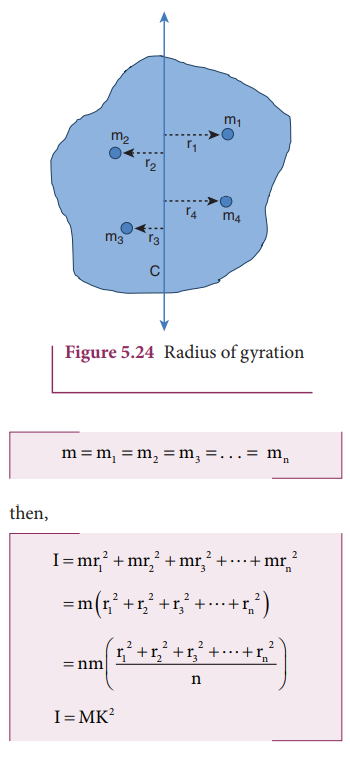
A
rotating rigid body with respect to any axis, is considered to be made up of
point masses m1, m2, m3, . . .mn at
perpendicular distances (or positions) r1, r2, r3
. . . rn respectively as shown in Figure 5.24.
The
moment of inertia of that object can be written as,
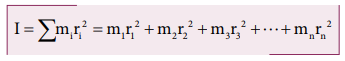
If
we take all the n number of individual masses to be equal,
where,
nm is the total mass M of the body and K is the radius of gyration.
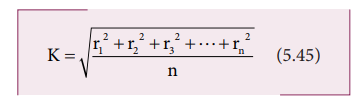
The expression for radius of
gyration indicates that it is the root mean square (rms) distance of the
particles of the body from the axis of rotation.
In
fact, the moment of inertia of any object could be expressed in the form, I = MK2.
For
example, let us take the moment of inertia of a uniform rod of mass M and
length l. Its moment of inertia with respect to a perpendicular axis
passing through the center of mass is, I= (1/12) Ml2

Theorems of Moment of Inertia
As
the moment of inertia depends on the axis of rotation and also the orientation
of the body about that axis, it is different for the same body with different
axes of rotation. We have two important theorems to handle the case of shifting
the axis of rotation.
(i) Parallel axis theorem:
Parallel axis theorem states that
the moment of inertia of a body about any axis is equal to the sum of its
moment of inertia about a parallel axis through its center of mass and the
product of the mass of the body and the square of the perpendicular distance
between the two axes.
If
IC is the moment of inertia of the body of mass M about an axis
passing through the center of mass, then the moment of inertia I about a
parallel axis at a distance d from it is given by the relation,
I = IC + Md2
(5.46)
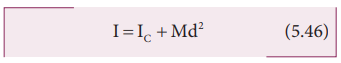
Let
us consider a rigid body as shown in Figure 5.25. Its moment of inertia about
an axis AB passing through the center of mass is IC. DE is another
axis parallel to AB at a perpendicular distance d from AB. The moment of
inertia of the body about DE is I. We attempt to get an expression for I in
terms of IC. For this, let us consider a point mass m on the body at
position x from its center of mass.
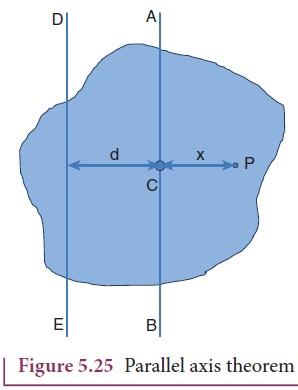
The
moment of inertia of the point mass about the axis DE is, m( x + d)2.
The
moment of inertia I of the whole body about DE is the summation of the above
expression.
I = + ∑ m (x+d)2
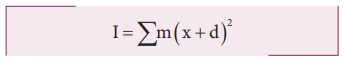
This
equation could further be written as,

Here,
∑mx2 is the moment of inertia of the body about
the center of mass. Hence, IC = ∑mx2
The
term, ∑mx = 0 because, x can take positive and
negative values with respect to the axis AB. The summation ( ∑mx) will be zero.
Thus,
I = IC + ∑md2 = IC + ( ∑m)d2
Here,
Σm is the entire mass M of the object ( ∑m = M )
I = IC + Md2
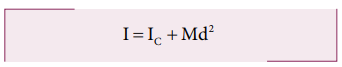
Hence,
the parallel axis theorem is proved.
(ii) Perpendicular axis theorem:
This
perpendicular axis theorem holds good only for plane laminar objects.
The theorem states that the moment
of inertia of a plane laminar body about an axis perpendicular to its plane is
equal to the sum of moments of inertia about two perpendicular axes lying in
the plane of the body such that all the three axes are mutually perpendicular
and have a common point.
Let
the X and Y-axes lie in the plane and Z-axis perpendicular to the plane of the
laminar object. If the moments of inertia of the body about X and Y-axes are IX and IY respectively and IZ
is the moment of inertia about Z-axis, then the perpendicular axis theorem
could be expressed as,
IZ =IX
+IY (5.47)
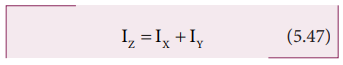
To
prove this theorem, let us consider a plane laminar object of negligible
thickness on which lies the origin (O). The X and Y-axes lie on the plane and
Z-axis is perpendicular to it as shown in Figure 5.26. The lamina is considered
to be made up of a large number of particles of mass m. Let us choose one such
particle at a point P which has coordinates (x, y) at a distance r from O.
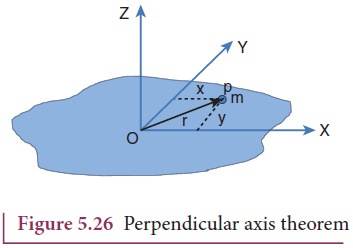
The
moment of inertia of the particle about Z-axis is, mr2
The
summation of the above expression gives the moment of inertia of the entire
lamina about Z-axis as, IZ
= ∑mr2
Here,
r2 = x2 + y2
Then,
IZ = ∑m ( x2 + y2 )
IZ = ∑m x2 + ∑m y2
IZ = ∑m x2 + ∑m y2
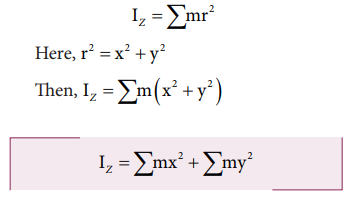
In
the above expression, the term Σmx 2 is the moment of
inertia of the body about the Y-axis and similarly the term Σmy2 is the moment of inertia about X-axis. Thus,
IX =∑my2
and
IY =∑mx2

Substituting
in the equation for Iz gives,
IZ = IX
+ IY
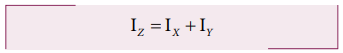
Thus,
the perpendicular axis theorem is proved.
Moment of Inertia of Different Rigid Bodies
The
moment of inertia of different objects about different axes is given in the
Table 5.3.

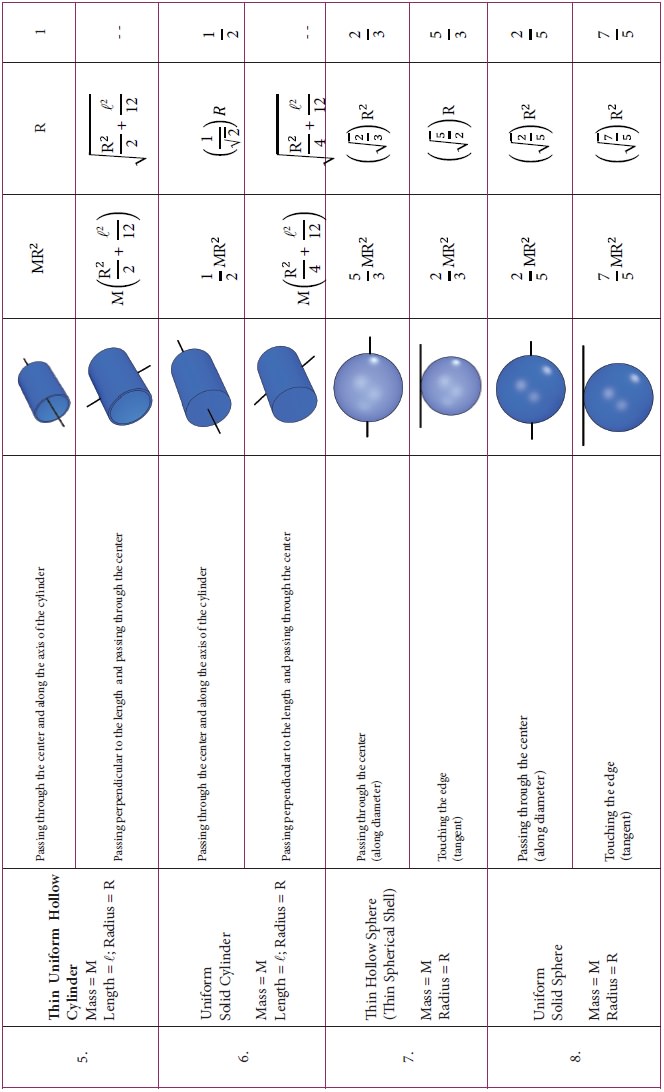
Solved Example Problems for Moment of Inertia of a Uniform Rod
Example 5.14
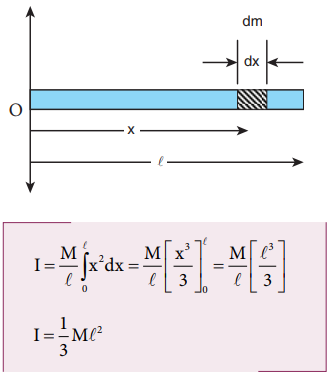
Find the moment of inertia of a uniform rod about an axis which is perpendicular to the rod and touches any one end of the rod.
Solution
The concepts to form the integrand to find the moment of inertia could be borrowed from the earlier derivation. Now, the origin is fixed to the left end of the rod and the limits are to be taken from 0 to ℓ.
Solved Example Problems for Radius of Gyration
Example 5.15
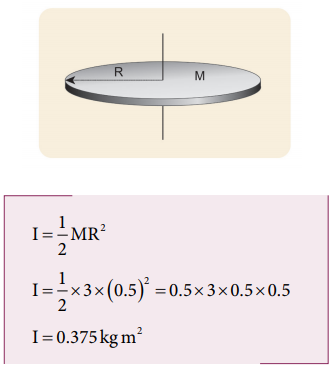
Find the radius of gyration of a disc of mass M and radius R rotating about an axis passing through the center of mass and perpendicular to the plane of the disc.
Solution
The moment of inertia of a disc about an axis passing through the center of mass and perpendicular to the disc is,I = ½ MR2

From the case of a rod and also a disc, we can conclude that the radius of gyration of the rigid body is always a geometrical feature like length, breadth, radius or their combinations with a positive numerical value multiplied to it.
Solved Example Problems for Theorems of Moment of Inertia
Example 5.16
Find the moment of inertia of a disc of mass 3 kg and radius 50 cm about the following axes.
i. axis passing through the center and perpendicular to the plane of the disc,
ii. axis touching the edge and perpendicular to the plane of the disc and
iii. axis passing through the center and lying on the plane of the disc.
Solution
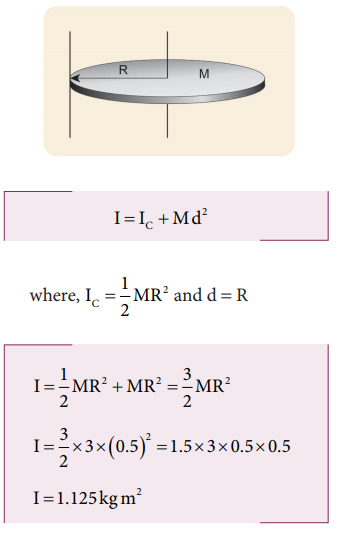
The mass, M = 3 kg, radius R = 50 cm = 50 × 10−2 m = 0.5 m
i. The moment of inertia (I) about an axis passing through the center and perpendicular to the plane of the disc is,
ii. The moment of inertia (I) about an axis touching the edge and perpendicular to the plane of the disc by parallel axis theorem is,
(iii) The moment of inertia (I) about an axis passing through the center and axis passing through the center and

About which of the above axis it is easier to rotate the disc?
It is easier to rotate the disc about an axis about which the moment of inertia is the least. Hence, it is case (iii).
Example 5.17
Find the moment of inertia about the geometric center of the given structure made up of one thin rod connecting two similar solid spheres as shown in Figure.

Solution
The structure is made up of three objects; one thin rod and two solid spheres.
The mass of the rod, M = 3 kg and the total length of the rod, ℓ = 80 cm = 0.8 m

The mass of the sphere, M = 5 kg and the radius of the sphere, R = 10 cm = 0.1 m

The moment of inertia of the sphere about geometric center of the structure is,
I sph = I C + Md2
Where, d = 40 cm + 10 cm = 50 cm = 0.5 m

As there are one rod and two similar solid spheres we can write the total moment of inertia (I) of the given geometric structure as, I = Irod + (2 × Isph )
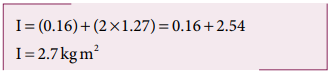
Related Topics