Solved Example Problems for Torque

Solved Example Problems for Torque

Example 5.7

If the force applied is perpendicular to the handle of the spanner as shown in the diagram, find the (i) torque exerted by the force about the center of the nut, (ii) direction of torque and (iii) type of rotation caused by the torque about the nut.

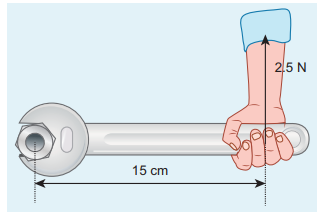
Solution

Arm length of the spanner, r = 15 cm = = 15×10−2m

Force, F = 2.5 N

Angle between r and F, θ = 90o

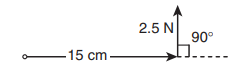
(i) Torque, τ θ = rF sin

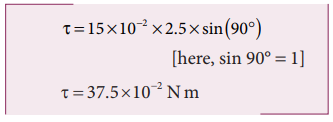
(ii) As  per  the  right  hand  rule,  the direction of torque is out of the page.

(iii) The type of rotation caused by the torque is anticlockwise.

Example 5.8

Example 5.9

A crane has an arm length of 20 m inclined at 30o with the vertical. It carries a container of mass of 2 ton suspended from the top end of the arm. Find the torque produced by the gravitational force on the container about the point where the arm is fixed to the crane. [Given: 1 ton = 1000 kg; neglect the weight of the arm. g = 10 ms-2]

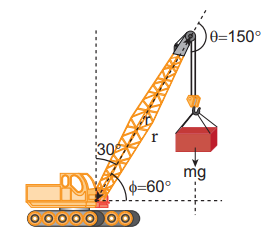
Solution

The force F at the point of suspension is due to the weight of the hanging mass.

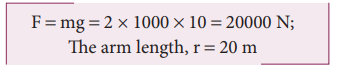
We can solve this problem by three different methods.

Method – I

The angle (θ) between the arm length (r) and the force (F) is, θ = 150o

The torque (τ) about the fixed point of the arm is,

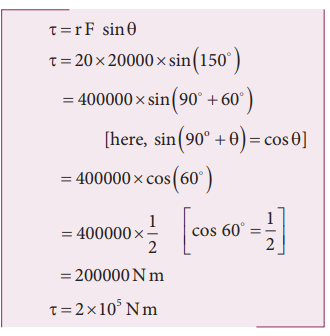
Method – II

Let us take the force and perpendicular distance from the point where the arm is fixed to the crane.

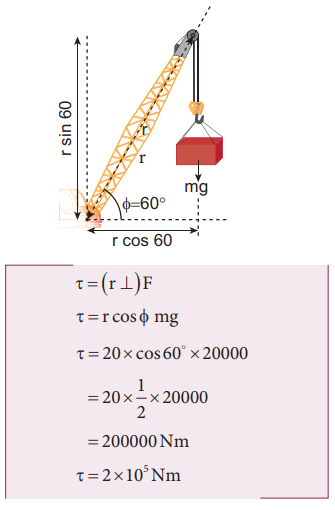
Method – III

Let us take the distance from the fixed point and perpendicular force.

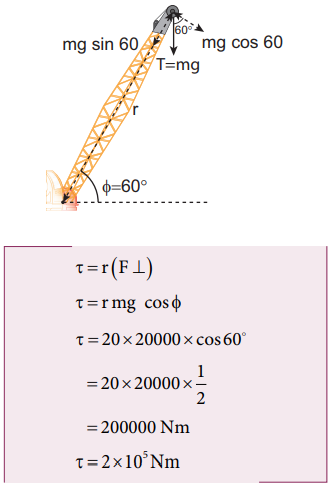
All the three methods, give the same answer

Solved Example Problems for Torque about an Axis

Example 5.10

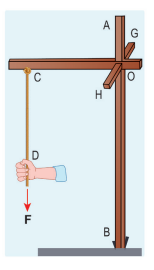
Three mutually perpendicular beams AB, OC, GH are fixed to form a structure which is fixed to the ground firmly as shown in the Figure. One string is tied to the point C and its free end D is pulled with a force F. Find the magnitude and direction of the torque produced by the force,

i. about the points D, C, O and B

ii. about the axes CD, OC, AB and GH.

Solution

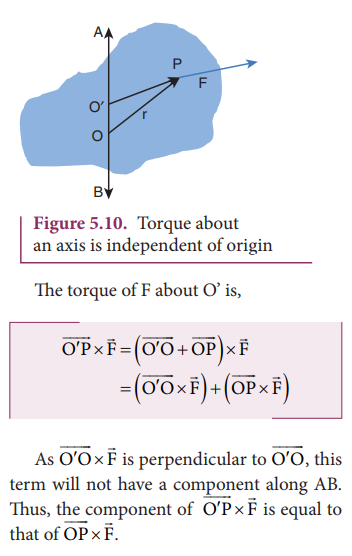
The torque of a force about an axis is independent of the choice of the origin as long as it is chosen on that axis itself. Th is can be shown as below. 

Let O be the origin on the axis AB, which is the rotational axis of a rigid body. F is the force acting at the point P. Now, choose another point O’ anywhere on the axis as shown in Figure 5.10.