Center of Mass for Distributed Point Masses

Center of Mass for Distributed Point Masses

A point mass is a hypothetical point particle which has nonzero mass and no size or shape. To find the center of mass for a collection of n point masses, say, m1, m2, m3 . . . mn we have to first choose an origin and an appropriate coordinate system as shown in Figure 5.2. Let, x1, x2, x3 . . . xn be the X-coordinates of the positions of these point masses in the X direction from the origin.

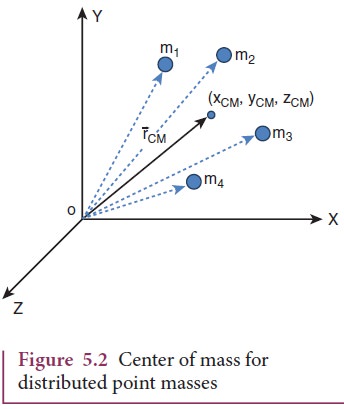
The equation for the X coordinate of the center of mass is,

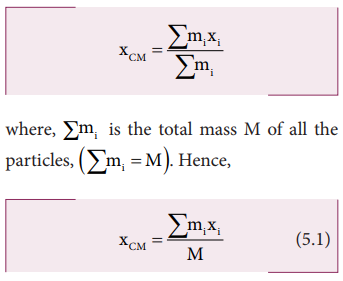
Similarly, we can also find y and z coordinates of the center of mass for these distributed point masses as indicated in Figure (5.2).

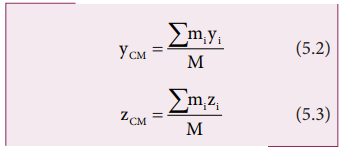
Hence, the position of center of mass of these point masses in a Cartesian coordinate system is (xCM, yCM, zCM). In general, the position of center of mass can be written in a vector form as,