Torque and Angular Acceleration

Torque and Angular Acceleration

Let us consider a rigid body rotating about a fixed axis. A point mass m in the body will execute a circular motion about a fixed axis as shown in Figure 5.11. A tangential force  acting on the point mass produces the necessary torque for this rotation. This force  is perpendicular to the position vector  of the point mass.

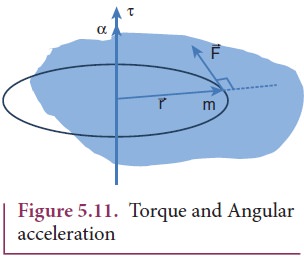
The torque produced by the force on the point mass m about the axis can be written as,

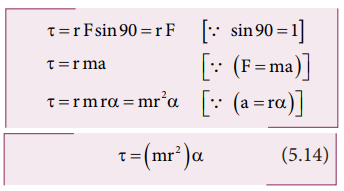
Hence, the torque of the force acting on the point mass produces an angular acceleration ( α) in the point mass about the axis of rotation.

In vector notation,

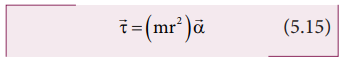
The directions of τ and α are along the axis of rotation. If the direction of τ is in the direction of α, it produces angular acceleration. On the other hand if, τ is opposite to α, angular deceleration or retardation is produced on the point mass.

The term mr2 in equations 5.14 and 5.15 is called moment of inertia (I) of the point mass. A rigid body is made up of many such point masses. Hence, the moment of inertia of a rigid body is the sum of moments of inertia of all such individual point masses that constitute the body ( I = ∑mi ri2 ). Hence, torque for the rigid body can be written as,

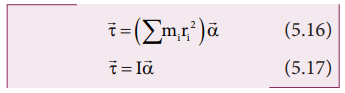
We will learn more about the moment of inertia and its significance for bodies with different shapes in section 5.4.