Physics - Slipping and Sliding | 11th Physics : UNIT 5 : Motion of System of Particles and Rigid Bodies
Chapter: 11th Physics : UNIT 5 : Motion of System of Particles and Rigid Bodies
Slipping and Sliding
Slipping and Sliding
When the round object moves, it always tends to roll on any surface which has a coefficient of friction any value greater than zero (µ > 0). The friction that enabling the rolling motion is called rolling friction. In pure rolling, there is no relative motion of the point of contact with the surface. When the rolling object speeds up or slows down, it must accelerate or decelerate respectively. If this suddenly happens it makes the rolling object to slip or slide.
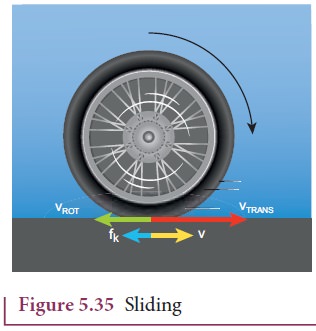
Sliding
Sliding is the case when vCM > Rω (or vTRANS > vROT). The translation is more than the rotation. This kind of motion happens when sudden break is applied in a moving vehicles, or when the vehicle enters into a slippery road. In this case, the point of contact has more of vTRANS than vROT. Hence, it has a resultant velocity v in the forward direction as shown in Figure 5.35. The kinetic frictional force (fk) opposes the relative motion. Hence, it acts in the opposite direction of the relative velocity. This frictional force reduces the translational velocity and increases the rotational velocity till they become equal and the object sets on pure rolling. Sliding is also referred as forward slipping.
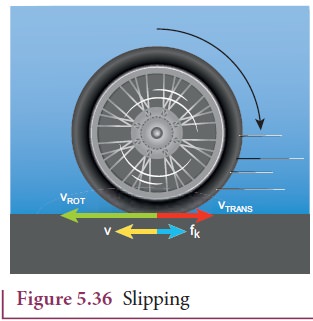
Slipping
Slipping is the case when vCM < Rω (or vTRANS < vROT). The rotation is more than the translation. This kind of motion happens when we suddenly start the vehicle from rest or the vehicle is stuck in mud. In this case, the point of contact has more of vROT than vTRANS. It has a resultant velocity v in the backward direction as shown in Figure 5.36. The kinetic frictional force (fk) opposes the relative motion. Hence it acts in the opposite direction of the relative velocity. This frictional force reduces the rotational velocity and increases the translational velocity till they become equal and the object sets pure rolling. Slipping is sometimes empahasised as backward slipping.
Solved Example Problems for Slipping and Sliding(Rolling Motion)
Example 5.21
A rolling wheel has velocity of its center of mass as 5 m s-1. If its radius is 1.5 m and angular velocity is 3 rad s-1, then check whether it is in pure rolling or not.
Solution
Translational velocity (vTRANS) or velocity of center of mass, vCM = 5 m s-1
The radius is, R = 1.5 m and the angular velocity is, ω = 3 rad s-1
Rotational velocity, vROT = Rω
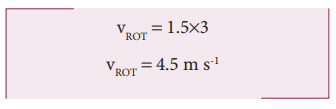
As vCM > Rω (or) vTRANS > Rω, It is not in pure rolling, but sliding.
Related Topics