Chapter: 11th Physics : UNIT 5 : Motion of System of Particles and Rigid Bodies
Solved Example Problems for Theorems of Moment of Inertia
Solved Example Problems for Theorems of Moment of Inertia
Example 5.16
Find the moment of inertia of a disc of mass 3 kg and radius 50 cm about the following axes.
i. axis passing through the center and perpendicular to the plane of the disc,
ii. axis touching the edge and perpendicular to the plane of the disc and
iii. axis passing through the center and lying on the plane of the disc.
Solution
The mass, M = 3 kg, radius R = 50 cm = 50 × 10−2 m = 0.5 m
i. The moment of inertia (I) about an axis passing through the center and perpendicular to the plane of the disc is,
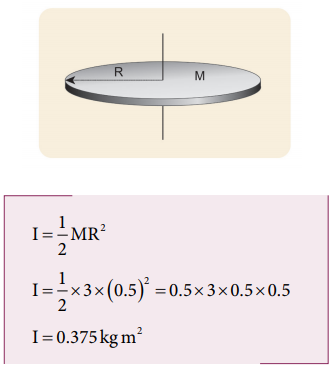
ii. The moment of inertia (I) about an axis touching the edge and perpendicular to the plane of the disc by parallel axis theorem is,
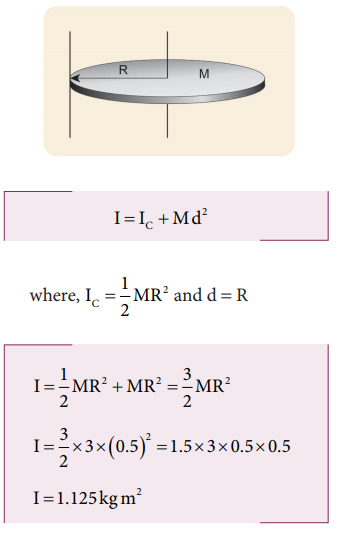
(iii) The moment of inertia (I) about an axis passing through the center and axis passing through the center and

About which of the above axis it is easier to rotate the disc?
It is easier to rotate the disc about an axis about which the moment of inertia is the least. Hence, it is case (iii).
Example 5.17
Find the moment of inertia about the geometric center of the given structure made up of one thin rod connecting two similar solid spheres as shown in Figure.

Solution
The structure is made up of three objects; one thin rod and two solid spheres.
The mass of the rod, M = 3 kg and the total length of the rod, ℓ = 80 cm = 0.8 m

The mass of the sphere, M = 5 kg and the radius of the sphere, R = 10 cm = 0.1 m

The moment of inertia of the sphere about geometric center of the structure is,
I sph = I C + Md2
Where, d = 40 cm + 10 cm = 50 cm = 0.5 m

As there are one rod and two similar solid spheres we can write the total moment of inertia (I) of the given geometric structure as, I = Irod + (2 × Isph )
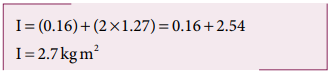
Related Topics