Chapter: 11th Physics : UNIT 5 : Motion of System of Particles and Rigid Bodies
Angular Momentum
Angular Momentum
The angular momentum in rotational motion is equivalent to linear momentum in translational motion. The angular momentum of a point mass is defined as the moment of its linear momentum. In other words, the angular momentum L of a point mass having a linear momentum p at a position r with respect to a point or axis is mathematically written as,
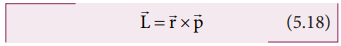
The magnitude of angular momentum could be written as,
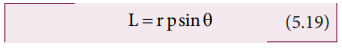
where, θ is the angle between ![]() and
and ![]() .
. ![]() is perpendicular to the plane containing
is perpendicular to the plane containing ![]() and
and ![]() . As we have written in the case of torque, here also we can associate sin θ with either
. As we have written in the case of torque, here also we can associate sin θ with either ![]() or
or ![]() .
.
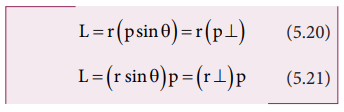
where, p⊥ is the component of linear momentum p perpendicular to r, and r⊥ is the component of position r perpendicular to p.
The angular momentum is zero ( L = 0 ), if the linear momentum is zero (p = 0) or if the particle is at the origin (![]() = 0) or if
= 0) or if ![]() and
and ![]() are parallel or antiparallel to each other (0 0 or 1800).
are parallel or antiparallel to each other (0 0 or 1800).
There is a misconception that the angular momentum is a quantity that is associated only with rotational motion. It is not true. The angular momentum is also associated with bodies in the linear motion. Let us understand the same with the following example.
Angular Momentum and Angular Velocity
Let us consider a rigid body rotating about a fixed axis. A point mass m in the body will execute a circular motion about the fixed axis as shown in Figure 5.12.
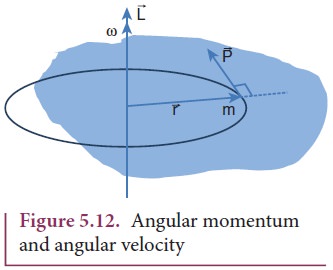
The point mass m is at a distance r from the axis of rotation. Its linear momentum at any instant is tangential to the circular path. Then the angular momentum ![]() is perpendicular to
is perpendicular to ![]() and
and ![]() . Hence, it is directed along the axis of rotation. The angle θ between
. Hence, it is directed along the axis of rotation. The angle θ between ![]() and
and ![]() in this case is 90o. The magnitude of the angular momentum L could be written as,
in this case is 90o. The magnitude of the angular momentum L could be written as,
L = rmv sin90o = rmv

where, v is the linear velocity. The relation between linear velocity v and angular velocity ω in a circular motion is, v = r ω. Hence,
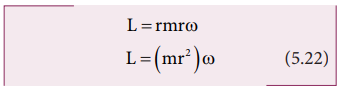
The directions of L and ω are along the axis of rotation. The above expression can be written in the vector notation as,

As discussed earlier, the term mr2 in equations 5.22 and 5.23 is called moment of inertia (I) of the point mass. A rigid body is made up of many such point masses. Hence, the moment of inertia of a rigid body is the sum of moments of inertia of all such individual point masses that constitute the body ( I = ∑mi ri 2 ). Hence, the angular momentum of the rigid body can be written as,
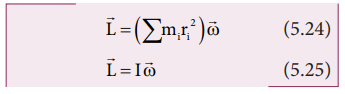
The study about moment of inertia (I) is reserved for Section 5.4.
Torque and Angular Momentum
We have the expression for magnitude of angular momentum of a rigid body as, L = I ω . The expression for magnitude of torque on a rigid body is, τ = I α
We can further write the expression for torque as,
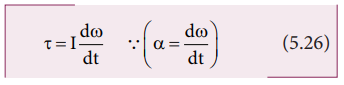
Where, ω is angular velocity and a is angular acceleration. We can also write equation 5.26 as,

The above expression says that an external torque on a rigid body fixed to an axis produces rate of change of angular momentum in the body about that axis.
This is the Newton’s second law in rotational motion as it is in the form of F = dp/dt which holds good for translational motion.
Conservation of angular momentum:
From the above expression we could conclude that in the absence of external torque, the angular momentum of the rigid body or system of particles is conserved.
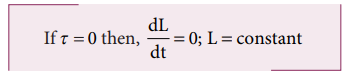
The above expression is known as law of conservation of angular momentum. We will learn about this law further in section 5.5.
Solved Example Problems for Angular Momentum
Example 5.11
A particle of mass (m) is moving with constant velocity (v). Show that its angular momentum about any point remains constant throughout the motion.
Solution

The term ( OQsinθ ) is the perpendicular distance (d) between the origin and line along which the mass is moving. Hence, the angular momentum of the particle about the origin is,
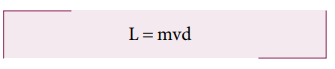
The above expression for angular momentum L, does not have the angle θ. As the momentum (p = mv) and the perpendicular distance (d) are constants, the angular momentum of the particle is also constant. Hence, the angular momentum is associated with bodies with linear motion also. If the straight path of the particle passes through the origin, then the angular momentum is zero, which is also a constant.
Related Topics