Choose the correct answers

1. The center of mass of a system of particles does not depend upon, 

(a) position of particles

(b) relative distance between particles

(c) masses of particles

(d) force acting on particle

Answer : d) force acting on particle

2. A couple produces, 

(a) pure rotation

(b) pure translation

(c) rotation and translation

(d) no motion

Answer : a) pure rotation

3. A particle is moving with a constant velocity along a line parallel to positive X-axis. The magnitude of its angular momentum with respect to the origin is, 

(a) zero

(b) increasing with x

(c) decreasing with x

(d) remaining constant

Answer : d) remaining constant

4. A rope is wound around a hollow cylinder of mass 3 kg and radius 40 cm. What is the angular acceleration of the cylinder if the rope is pulled with a force 30 N? 

(a) 0.25 rad s–2

(b) 25 rad s–2

(c) 5 m s–2

(d) 25 m s–2.

Answer : b) 25 rad s^-2

Solution:

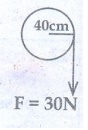
τ = Iα ;

F × R = MR²α

30 × 0.4 = 3(0.4)²α

12 = 3 × 0.16α

400 =16 α

α = 25rad s^-2

5. A closed cylindrical container is partially filled with water. As the container rotates in a horizontal plane about a perpendicular bisector, its moment of inertia, 

(a) increases

(b) decreases

(c) remains constant

(d) depends on direction of rotation.

Answer: a) increases

6. A rigid body rotates with an angular momentum L. If its kinetic energy is halved, the angular momentum becomes, 

(a) L

(b) L/2

(c) 2L

(d) L/ 2

Answer: d) L/√2

Solution:

L² = 2I(KE) ;

KE = Half

L² = 2I (KE / 2)

L² = L² / 2

L² = 2I × [ L² / 2I ] × [ 1/2 ]

L = √[L² / 2] 

L = L / √2

7. A particle undergoes uniform circular motion. The angular momentum of the particle remain conserved about, 

(a) the center point of the circle.

(b) the point on the circumference of the circle.

(c) any point inside the circle.

(d) any point outside the circle.

Answer : a) the center point of the circle

8. When a mass is rotating in a plane about a fixed point, its angular momentum is directed along, 

(a) a line perpendicular to the plane of rotation

(b) the line making an angle of 45° to the plane of rotation

(c) the radius

(d) tangent to the path

Answer : a) a line perpendicular to the plane of rotation

9. Two discs of same moment of inertia rotating about their regular axis passing through center and perpendicular to the plane of disc with angular velocities ω1 and ω2. They are brought in to contact face to face coinciding the axis of rotation. The expression for loss of energy during this process is, 

(a) 1/4 I (ω1- ω2)2

(b) I (ω1- ω2)2

(c) 1/8 I (ω1- ω2)2

(d) 1/2 I (ω1- ω2)2 

Answer: a) 1/4 I (ω₁ – ω₂)²

Solution:

Δ KE = 1/2 ([I₁ I₂] / [I₁ + I₂]) (ω₁ – ω₂)²

= 1/2 (I ² / (2I)) (ω₁ – ω₂)²

= 1/4 I (ω₁ – ω₂)²

10. A disc of moment of inertia Ia is rotating in a horizontal plane about its symmetry axis with a constant angular speed ω. Another discinitially at rest of moment of inertia Ib is dropped coaxially on to the rotating disc. Then, both the discs rotate with same constant angular speed. The loss of kinetic energy due to friction in this process is,

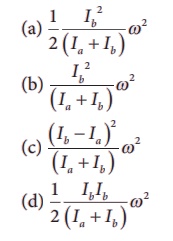
Answer: d) 1/2 { [I_bI_b] / (I_a + I_b) } ω²

Solution:

L_i = L_f

I_aω_a = I_fω_f

I_aω_a = (I_a+I_b)ω_f

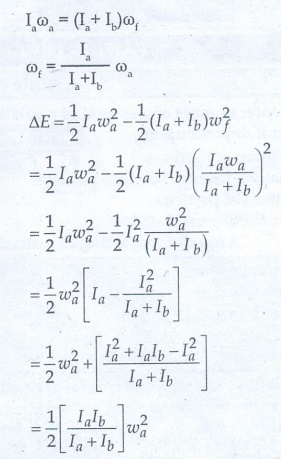
11. The ratio of the acceleration for a solid sphere (mass m and radius R) rolling down an incline of angle θ without slipping and slipping down the incline without rolling is, 

(a) 5:7

(b)2:3

(c) 2:5

(d) 7:5

Answer: a) 5:7

Solution:

a₁ = [ g sin θ ] / [ 1 + K²/r² ]

a₂ = g sin θ

a₁ / a₂ = 1 / { 1 + K²/r² } = 1 / { 1 + 2/5} = 5 / 7 = 5 : 7

12. From a disc of radius R a mass M, a circular hole of diameter R, whose rim passes through the center is cut. What is the moment of inertia of the remaining part of the disc about a perpendicular axis passing through it 

(a) 15MR2/32

(b) 13MR2/32

(c) 11MR2/32

(d) 9MR2/32

Answer: b) 13 MR² / 32

Solution:

M.I of total disc about perpendicular axis

I_r = 1/2 MR²

Mass of the removed portion

M₁ = [ M / 4πR² ] × 4π(R/2)² = M / 4

Moment of inertia of a removed disc

I_R = [ 1/2 M₁(R/2)² ] + [ M₁(R/2)² ]

= [ 1/2 M/4 R²/4 ] + [ MR² / 16 ] = 3/32 MR²

M.I of the remaining portion

I_Remain = I_r − I_R = 1/2 MR² – 3/32 MR² = 13/32 MR²

13. The speed of a solid sphere after rolling down from rest without sliding on an inclined plane of vertical height h is,

Ans: a

Answer: a / b) √[ (4 / 3) gh ] / √[ (10 / 7) gh ]

14. The speed of the center of a wheel rolling on a horizontal surface is vo. A point on the rim in level with the center will be moving at a speed of speed of, 

(a) zero

(b) vo

(c) √2vo

(d) 2vo

Answer : c) √(2 v_o)

Solution: v = √[ V₀² + V² ]

v = √[2V₀²]

v = √2 V₀

15. A round object of mass M and radius R rolls down without slipping along an inclined plane. The fractional force, 

(a) dissipates kinetic energy as heat.

(b) decreases the rotational motion.

(c) decreases the rotational and transnational motion

(d) converts transnational energy into rotational energy

Answer : d) converts translational energy into rotational energy

Answers:

1) d 2) a 3) d 4) b

5) a 6) d 7) a 8) a

9) a 10) d 11) a 12) b

13) a 14) c 15) d