Rolling on Inclined Plane

Rolling on Inclined Plane

Let us assume a round object of mass m and radius R is rolling down an inclined plane without slipping as shown in Figure 5.37. There are two forces acting on the object along the inclined plane. One is the component of gravitational force (mg sinθ) and the other is the static frictional force (f). The other component of gravitation force (mg cosθ) is cancelled by the normal force (N) exerted by the plane. As the motion is happening along the incline, we shall write the equation for motion from the free body diagram (FBP) of the object.

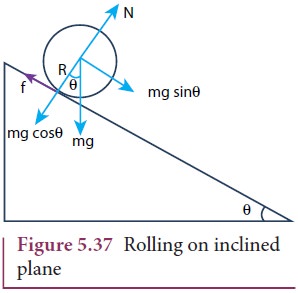
For translational motion, mg sinθ is the supporting force and f is the opposing force,

 mg sinθ - f = ma          (5.61)

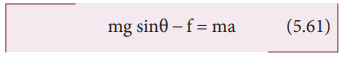
 For rotational motion, let us take the torque with respect to the center of the object. Then mg sinθ cannot cause torque as it passes through it but the frictional force f can set torque of Rf.

Rf  = Iα

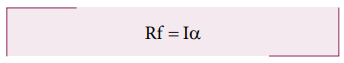
By using the relation, a = r α, and moment of inertia I = mK2, we get,

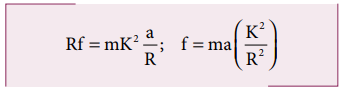
Now equation (5.59) becomes,

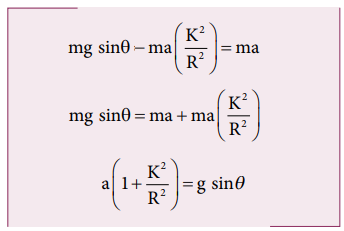
After rewriting it for acceleration, we get,

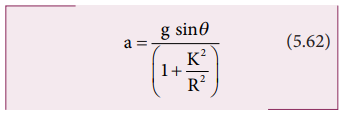
We can also find the expression for final velocity of the rolling object by using third equation of motion for the inclined plane. v 2 = u2 + 2as. If the body starts rolling from rest, u = 0. When h is the vertical height of the incline, the length of the incline s is, s = h/sinθ

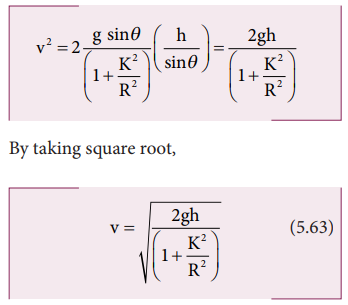
The time taken for rolling down the incline could also be written from first equation of motion as, v = u + at. For the object which starts rolling from rest, u = 0. Then,

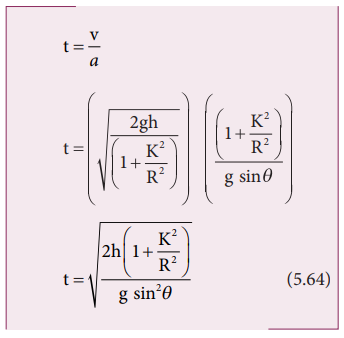
The equation suggests that for a given incline, the object with the least value of radius of gyration K will reach the bottom of the incline first.

Solved Example Problems for Rolling on Inclined Plane(Rolling Motion)

Example 5.23

Four round objects namely a ring, a disc, a hollow sphere and a solid sphere with same radius R start to roll down an incline at the same time. Find out which object will reach the bottom first.

Solution

For all the four objects namely the ring, disc, hollow sphere and solid sphere, the radii of gyration K are R, √(1/2) R, √(2/3) R, √(2/5) R (ref Table (5.3)). With numerical values the radius of gyration K are 1R, 0.707R, 0.816R, 0.632R respectively. The expression for time taken for rolling has the radius of gyration K in the numerator as per equation 5.63

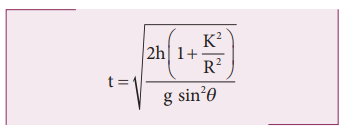
The one with least value of radius of gyration K will take the shortest time to reach the bottom of the inclined plane. The order of objects reaching the bottom is first, solid sphere; second, disc; third, hollow sphere and last, ring.