Chapter: 11th Physics : UNIT 5 : Motion of System of Particles and Rigid Bodies
Kinetic Energy in Pure Rolling
Kinetic Energy in Pure Rolling
As pure is the combination of translational and rotational motion, we can write the total kinetic energy (KE) as the sum of kinetic energy due to translational motion (KETRANS) and kinetic energy due to rotational motion (KEROT).

If the mass of the rolling object is M, the velocity of center of mass is vCM, its moment of inertia about center of mass is ICM and angular velocity is ω, then

With center of mass as reference:
The moment of inertia (ICM) of a rolling object about the center of mass is,
I CM = MK2 and vCM = Rω. Here, K is radius of gyration.
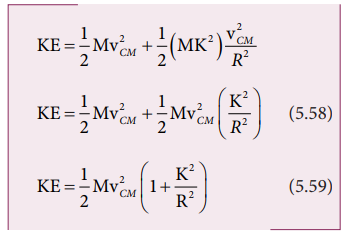
With point of contact as reference:
We can also arrive at the same expression by taking the momentary rotation happening with respect to the point of contact (another approach to rolling). If we take the point of contact as O, then,
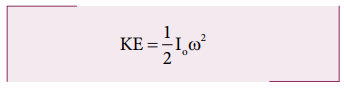
Here, Io is the moment of inertia of the object about the point of contact. By parallel axis theorem, I o = I CM + MR2. Further we can write, Io = MK2 + MR2. With vCM = Rω or ω = VCM/R.
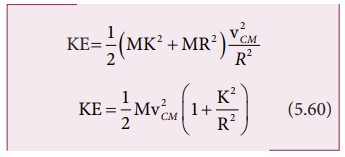
As the two equations 5.59 and 5.60 are the same, it is once again confirmed that the pure rolling problems could be solved by considering the motion as any one of the following two cases.
i. The combination of translational motion and rotational motion about the center of mass. (or)
ii. The momentary rotational motion about the point of contact.
Solved Example Problems for Kinetic Energy in Pure Rolling(Rolling Motion)
Example 5.22
A solid sphere is undergoing pure rolling. What is the ratio of its translational kinetic energy to rotational kinetic energy?
Solution
The expression for total kinetic energy in pure rolling is,
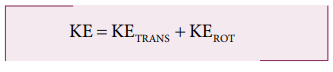
For any object the total kinetic energy as per equation 5.58 and 5.59 is,
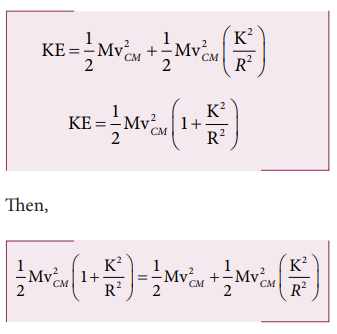
The above equation suggests that in pure rolling the ratio of total kinetic energy, translational kinetic energy and rotational kinetic energy is given as,

Related Topics