Long Questions and Answer

Motion of System of Particles and Rigid Bodies (Physics)

Long Answer Questions

1. Explain the types of equilibrium with suitable examples.

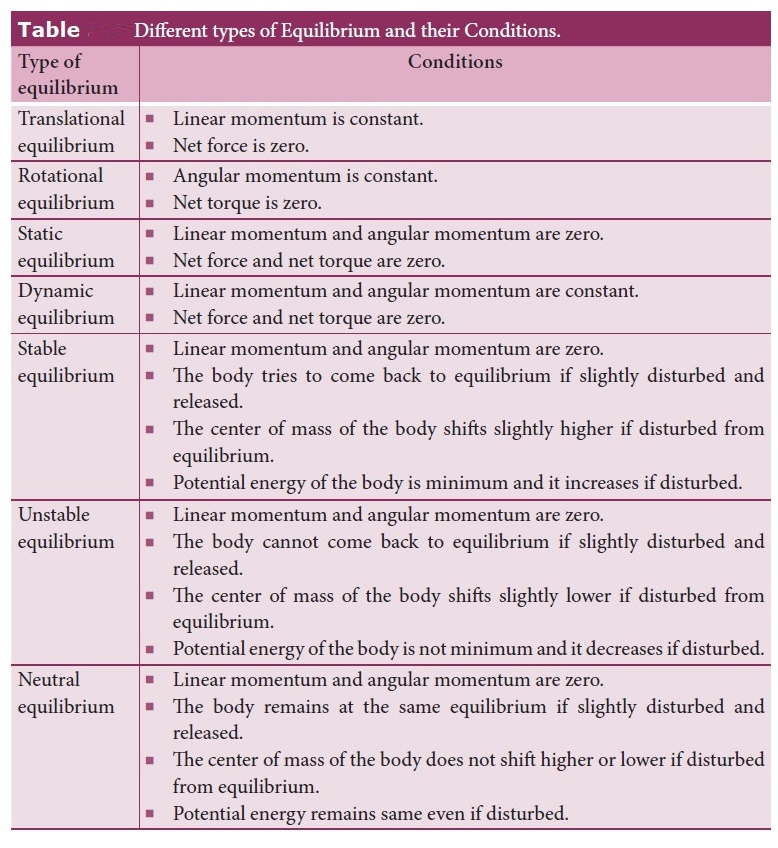
2. Explain the method to find the center of gravity of a irregularly shaped lamina.

● It is a measure of how difficult it is to rotate a particular body about a given axis.

● The vertical line is marked as PP’.

● Suspend the body through other points like Q and R.

● Mark the vertical line as QQ' and RR’.

● The intersection of the vertical (G) gives the centre of gravity of a irregularly shaped lamina.

3. Explain why a cyclist bends while negotiating a curve road? Arrive at the expression for angle of bending for a given velocity.

● Let us consider a cyclist negotiating a circular level road of radius ‘r’ with a speed ‘v’.

● The cycle and the cyclist are considered as one system with mass m.

● C' is center of gravity, ‘r’ -radius of circle with center at ‘o’

● The line OC are x axis, and the vertical line through O as Z axis

● The system is at rest in this rotating frame.

The force acting on the system are

i) gravitational force (mg)

ii) normal force (N)

iii) frictional force (f) and

iv) centrifugal force (pseudo force) which acts through center of gravity.

● The System is in equlibrium in the rotational frames of reference.

F_net = 0 ;

τ_net = 0

● The torque due to gravitational force about point A = −mgAB (Clockwise)

● The torque due to centripetal force = mv² / r (BC) (anti clockwise)

● −mgAB + mv²/r BC = 0 ; mgAB = mv²/r BC

From ∆ ABC

AB = AC sin θ

BC = AC cos θ

mg AC sin θ = [ mv² / r ] AC cosθ

tanθ = v² / rg

θ = tan^-1 (v² / rg)

A cyclist has to bend by an angle θ to stay in equilibrium.

4. Derive the expression for moment of inertia of a rod about its center and perpendicular to the rod.

● First an origin is to be fixed for the coordinate system which is also the geometric centre of the rod.

● The rod is now along x axis.

● An infinitesimally small mass (dm) at a distance x from origin.

∴ dI = dm x²

∴ I = mr²

● Mass per unit length λ = m/ℓ

● Mass of length dx = dm = λ.dx = (m/ℓ) dx

● Moment of inertia of entire rod, I = ʃ dI

 = ʃ dmx²

 I = ʃ ( m/ℓ dx ) . x²

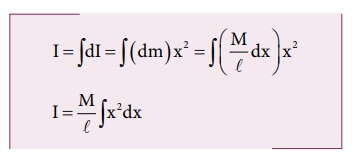
● As the mass is distributed on either side, limits taken from −ℓ/2 to ℓ/2 .

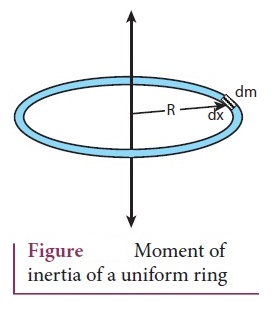
5. Derive the expression for moment of inertia of a uniform ring about an axis passing through the center and perpendicular to the plane.

● Let us consider a uniform ring of mass M and radius R.

● dm - infinitesimal small mass (dm) of length (dx)

R - Radius of the ring from the axis.

dI = (dm) R²

● The Length of the ring = 2πR (Circumference)

● Mass per unit length λ = M / 2πR

● Mass of length dx, dm = λdx

dm = (M / 2πR) dx

● Moment of inertia I = ʃ dI

 = ʃ (dm) R²

 I = [MR / 2π] ʃ dx

To cover entire length limits taken from 0 to 2πR

I = (MR / 2π ) ʃ ^2πR₀ dx

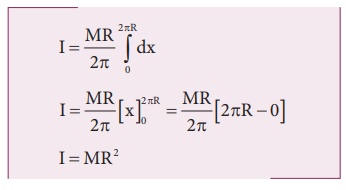
I = (MR / 2π) (x)^2πR₀ ; I = (MR / 2π) (2πR-0)

 I = MR²

6. Derive the expression for moment of inertia of a uniform disc about an axis passing through the center and perpendicular to the plane.

Consider a disc of mass M and radius R. This disc is mad up of many infinite simally small rings

dI = (dm) r²

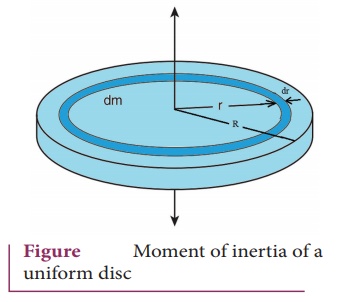
Mass per unit area σ = M / πR²

Mass of small ring

dm = σ 2πrdr

dm = [ M/πR² ] 2πrdr

Where 2πrdr is the area of this element ring

dm = 2M / R² (rdr)

dI = 2M / R² (r³dr)

I = ʃ dI

 = [2M / R² ] ^Rʃ₀r³dr

I = 2M / R² [ r⁴ / 4]^R₀ = 2M / R² [ R⁴/4 - 0]

I = ½ MR²

7. Discuss conservation of angular momentum with example.

● When no external torque acts on the body the net angular momentation of a rotating rigid body remains conslant.

τ = dL / dt

If τ = 0

L = constant

(ie) Iω = constant

● I increases ω will decrease and vice-versa. Example: The ice dancer

● The dancer spins slowly when the hands are stretched out and spins faster when the hands are brought close to the body.

● Stretching of hands away from body increases moment of inertia, thus the angular velocity decreases resulting in slower spin.

● When the hands are brought close to the body, the moment of inertia decreases, and thus the angular velocity increases resulting in faster spin.

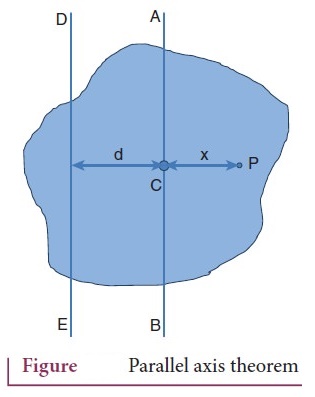
8. State and prove parallel axis theorem.

Statement: Parallel axis theorem states that the moment of inertia of a body about any axis (I) is equal to the sum of its moment of inertia about a parallel axis through its center of mass (I) and the product of the mass of the body and the square of the perpendicular distance between the two axes (Md²).

I = I_c + Md²

I = I_c + (Σm) d²

Proof:

● Let us consider a rigid body as shown in Figure

● Its moment of inertia about an axis AB passing through the center of mass is I_c.

● DE is another axis parallel to AB at a perpendicular distance d from AB. The moment of inertia of the body about DE is I.

● let us consider a point mass m on the body at position x from its center of mass.

● The moment of inertia of the point mass about the axis DE is = m(x + d)².

● The moment of inertia I of the whole body about

DE, I = Σm(x+d)²

I = Σm(x² + d² + 2xd)

= Σ(mx²+rnd²+2dmx)

I = Σmx² + Σmd² + 2dΣmx

Here,

I_c = Σmx² (moment of inertia of the body about the center of mass)

Σmx = O (because, x can take positive and negative values with respect to the axis AB.)

∴ I = I_c + (Σm)d²

Where,

Σm = M

I = I_c + Md²

Hence parallel axis theorem is proved.

9. State and prove perpendicular axis theorem.

Statement: The moment of inertia of a plane laminar body about an axis perpendicular to its plane is equal to the sum of moment of inertia about two perpendicular axes lying in the plane of the body such that all the three axes are mutually perpendicular and have a common point.

I_z = I_x + I_y

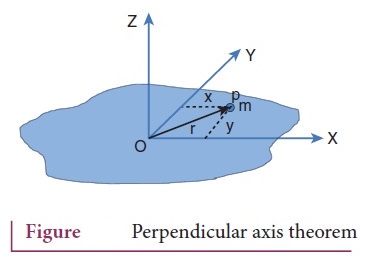
Proof :

● let us consider a plane laminar object of negligible thickness on which lies the origin (O).

● The X and Y-axes lie on the plane and Z-axis is perpendicular to it.

● The laminar is considered to be made up of a large number of particles of mass m. Let us choose one such particle at a point P which has coordinates (x, y) at a distance r from O.

● The moment of inertia of the particle about Z axis = mr²

● The moment of inertia of the entire laminar about Z axis I_z = Σmr²

r² = x² + y²

I_z = Σm (x² + y²)

I_z = Σmx² + Σmy²          ………… (1)

where

Σmx² - moment of intertia of the body about the y axis.

Σmy² - moment of intertia of the body about the x axis.

I_x = Σmy²            ……….. (2)

I_y = Σmx²              ……….. (3)

Substituting (2) and (3) in the equation (1)

I_z = I_x + I_y

The perpendicular axis theorem is proved.

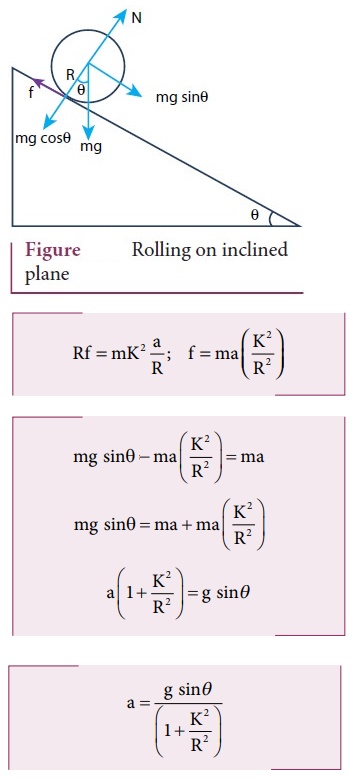
10. Discuss rolling on inclined plane and arrive at the expression for the acceleration.

● Let us assume a round object of mass m and radius R is rolling down an inclined plane without slipping

● There are two forces acting on the object

i) gravitational force (mg sinθ)

ii) static frictional force (f).

● The other component of gravitational force (mg cosθ) is cancelled by the normal force (N) exerted by the plane.

● For translational motion, mg sinθ is the supporting force and f is the opposing force,

mg sinθ - f = ma          ………. (1)

● For rotational motion, let us take the torque with respect to the center of the object.

● Then mg sinθ cannot cause torque as it passes through it but the frictional force f can set torque of Rf.

Rf = Iα

a = rα

I = mk²

Rf = mk²(a/R)

f = m (K² / R²) a              …………(2)

Sub (2) in (1)

mg sinθ – ma (K² / R²) = ma

mg sinθ = ma + ma (K² / R²)

a ( 1 + K²/R² ) = g sin θ

a = [ g sin θ ] / [ (1 + K² / R²) ]