Combination of Translation and Rotation

Combination of Translation and Rotation

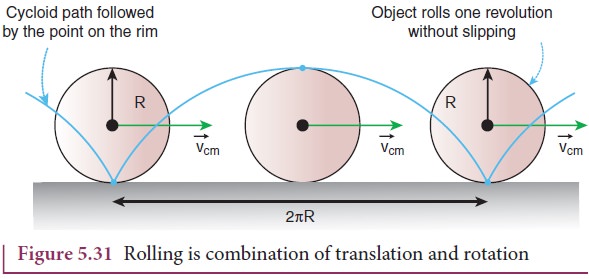
We will now see how these translational and rotational motions are related in rolling. If the radius of the rolling object is R, in one full rotation, the center of mass is displaced by 2πR (its circumference). One would agree that not only the center of mass, but all the points on the disc are displaced by the same 2πR after one full rotation. The only difference is that the center of mass takes a straight path; but, all the other points undergo a path which has a combination of the translational and rotational motion. Especially the point on the edge undergoes a path of a cycloid as shown in the Figure 5.31.

As the center of mass takes only a straight line path, its velocity vCM is only translational velocity vTRANS (vCM = vTRANS). All the other points have two velocities. One is the translational velocity vTRANS, (which is also the velocity of center of mass) and the other is the rotational velocity vROT (vROT = rω). Here, r is the distance of the point from the center of mass and ω is the angular velocity. The rotational velocity vROT is perpendicular to the instantaneous position vector from the center of mass as shown in Figure 5.32(a) . The resultant of these two velocities is v. This resultant velocity v is perpendicular to the position vector from the point of contact of the rolling object with the surface on which it is rolling as shown in Figure 5.32(b).

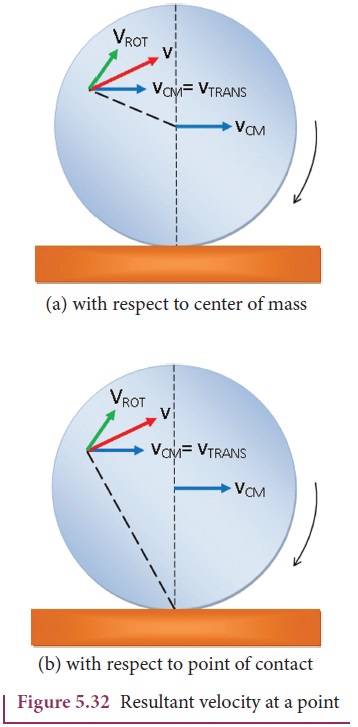
We shall now give importance to the point of contact. In pure rolling, the point of the rolling object which comes in contact with the surface is at momentary rest. This is the case with every point that is on the edge of the rolling object. As the rolling proceeds, all the points on the edge, one by one come in contact with the surface; remain at momentary rest at the time of contact and then take the path of the cycloid as already mentioned.

Hence, we can consider the pure rolling in two different ways.

i. The combination of translational motion and rotational motion about the center of mass.

Or

ii. The momentary rotational motion about the point of contact.

As the point of contact is at momentary rest in pure rolling, its resultant velocity v is zero (v = 0). For example, in Figure 5.33, at the point of contact, vTRANS is forward (to right) and vROT is backwards (to the left).

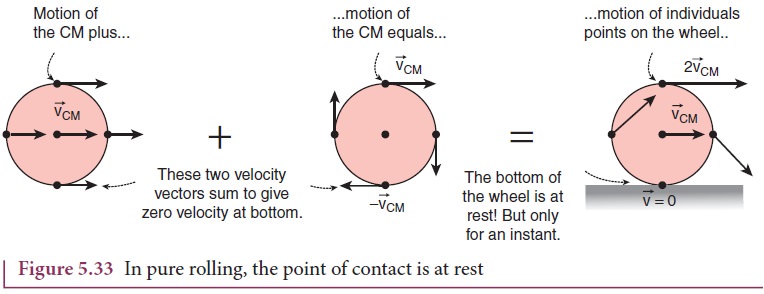
That implies that, v TRANS and vROT are equal in magnitude and opposite in direction (v = vTRANS- vROT = 0). Hence, we conclude that in pure rolling, for all the points on the edge, the magnitudes of vTRANS and vROT are equal (vTRANS= vROT). As vTRANS = vCM and vROT = Rω, in pure rolling we have,

vCM = Rω          (5.55)

We should remember the special feature of the equation 5.55. In rotational motion, as per the relation v = rω, the center point will not have any velocity as r is zero. But in rolling motion, it suggests that the center point has a velocity vCM given by equation 5.55.

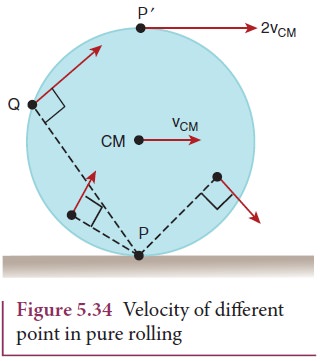
For the topmost point, the two velocities vTRANS and vROT are equal in magnitude and in the same direction (to the right). Thus, the resultant velocity v is the sum of these two velocities, v = vTRANS + v ROT. In other form, v = 2 vCM as shown in Figure 5.34.