Chapter: 11th Physics : UNIT 5 : Motion of System of Particles and Rigid Bodies
Effect of Torque on Rigid Bodies
Effect of Torque on Rigid Bodies
A rigid body which has non zero external torque ( τ) about the axis of rotation would have an angular acceleration ( α) about that axis. The scalar relation between the torque and angular acceleration is,
τ = I α (5.48)
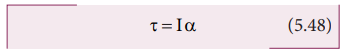
where, I is the moment of inertia of the rigid body. The torque in rotational motion is equivalent to the force in linear motion.
Solved Example Problems for Effect of Torque on Rigid Bodies
Example 5.18
A disc of mass 500 g and radius 10 cm can freely rotate about a fixed axis as shown in Figure A. light and inextensible string is wound several turns around it and 100 g body is suspended at its free end. Find the acceleration of this mass. [Given: The string makes the disc to rotate and does not slip over it. g = 10 m s-2.]
Solution

Let the mass of the disc be m1 and its radius R. The mass of the suspended body is m2.
As the light inextensible string is wound around the disc several times it makes the disc rotate without slipping over it. The translational acceleration of m2 and tangential acceleration of m1 will be the same. Let us draw the free body diagram (FBD) of m1 and m2 separately.
FBD of the disc:
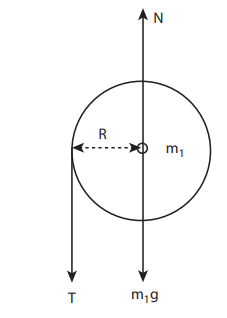
Its gravitational force (m1g) acts downward and normal force N exerted by the fixed support at the center acts upward. The tension T acts downward at the edge. The gravitational force (m1g) and the normal force (N) cancel each other. m1g = N
The tension T produces a torque (R T), which produces a rotational motion in the disc with angular acceleration, (α=a/R)
Here, a is the linear acceleration of a point at the edge of the disc. If the moment of inertia of the disc is I and its radius of gyration is K, then
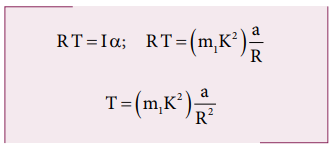
FBD of the body:
Its gravitational force (m2g) acts downward and the tension T acts upward. As (T < m2g), there is a resultant force (m2a) acting on it downward.
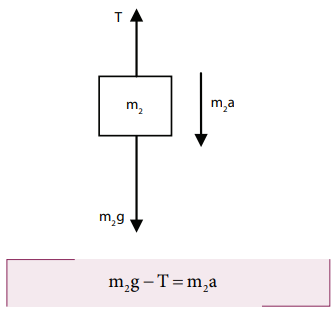
Substituting for T from the equation for disc,

Related Topics