Chapter: 11th Physics : UNIT 5 : Motion of System of Particles and Rigid Bodies
Motion of Center of Mass
Motion of Center of Mass
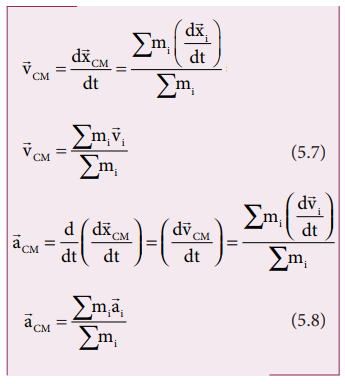
When a rigid body moves, its center of mass will also move along with the body. For kinematic quantities like velocity ( vCM ) and acceleration ( aCM ) of the center of mass, we can differentiate the expression for position of center of mass with respect to time once and twice respectively. For simplicity, let us take the motion along X direction only.
In the absence of external force, i.e. 
ext = 0, the individual rigid bodies of a system can move or shift only due to the internal forces. This will not affect the position of the center of mass. This means that the center of mass will be in a state of rest or uniform motion. Hence, 
CM will be zero when center of mass is at rest and constant when center of mass has uniform motion (CM =0 or CM = constant) There will be no acceleration of center of mass, (
CM =0).
From equation 5.7 and 5.8,
Here, the individual particles may still move with their respective velocities and accelerations due to internal forces.
In the presence of external force, (i.e. ext ≠ 0), the center of mass of the system will accelerate as given by the following equation.
Center of mass in explosions:
Many a times rigid bodies are broken in to fragments. If an explosion is caused by the internal forces in a body which is at rest or in motion, the state of the center of mass is not affected. It continues to be in the same state of rest or motion. But, the kinematic quantities of the fragments get affected. If the explosion is caused by an external agency, then the kinematic quantities of the center of mass as well as the fragments get affected.
Solved Example Problems for Motion of Center of Mass
Example 5.5
A man of mass 50 kg is standing at one end of a boat of mass 300 kg floating on still water. He walks towards the other end of the boat with a constant velocity of 2 ms-1 with respect to a stationary observer on land. What will be the velocity of the boat, (a) with respect to the stationary observer on land? (b) with respect to the man walking in the boat?
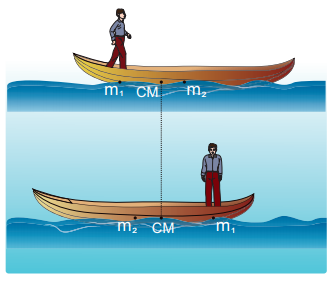
[Given: There is friction between the man and the boat and no friction between the boat and water.]
Solution
Mass of the man (m1) is, m1= 50 kg
Mass of the boat (m2) is, m2 = 300 kg
With respect to a stationary observer:
The man moves with a velocity, v1 = 2 m s-1 and the boat moves with a velocity v2 (which is to be found)
(i) To determine the velocity of the boat with respect to a stationary observer on land:
As there is no external force acting on the system, the man and boat move due to the friction, which is an internal force in the boat-man system. Hence, the velocity of the center of mass is zero (vCM = 0).
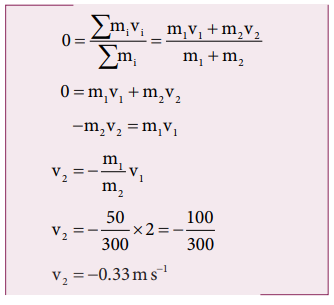
The negative sign in the answer implies that the boat moves in a direction opposite to that of the walking man on the boat to a stationary observer on land.
(ii) To determine the velocity of the boat with respect to the walking man:
We can find the relative velocity as,
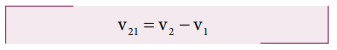
where, v21 is the relative velocity of the boat with respect to the walking man.
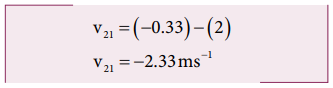
The negative sign in the answer implies that the boat appears to move in the opposite direction to the man walking in the boat.
The magnitude of the relative velocity of the boat with respect to the walking man is greater than the magnitude of the relative velocity of the boat with respect to the stationary observer.
The negative signs in the two answers indicate the opposite direction of the boat with respect to the stationary observer and the walking man on the boat.
Example 5.6
A projectile of mass 5 kg, in its course of motion explodes on its own into two fragments. One fragment of mass 3 kg falls at three fourth of the range R of the projectile. Where will the other fragment fall?
Solution
It is an explosion of its own without any external influence. After the explosion, the center of mass of the projectile will continue to complete the parabolic path even though the fragments are not following the same parabolic path. After the fragments have fallen on the ground, the center of mass rests at a distance R (the range) from the point of projection as shown in the diagram.
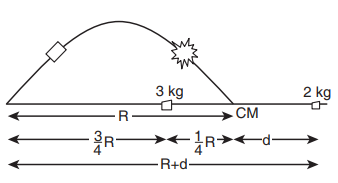
If the origin is fixed to the final position of the center of mass, the principle of moments holds good.
The other fragment falls at a distance of 1.375R from the point of launching. (Here R is the range of the projectile.)
Related Topics