Principle of Moments

Principle of Moments

Consider a light rod of negligible mass which is pivoted at a point along its length. Let two parallel forces F1 and F2 act at the two ends at distances d1 and d2 from the point of pivot and the normal reaction force N at the point of pivot as shown in Figure 5.15. If the rod has to remain stationary in horizontal position, it should be in translational and rotational equilibrium. Then, both the net force and net torque must be zero.

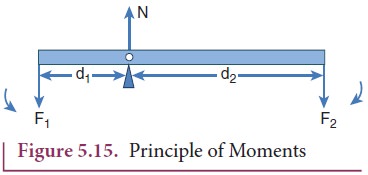
For net force to be zero, − F1 + N − F2 = 0

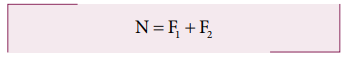
For net torque to be zero, d1F1 − d2 F2 = 0

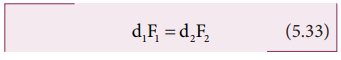
The above equation represents the principle of moments. This forms the principle for beam balance used for weighing goods with the condition d1 = d2; F1 = F2. We can rewrite the equation 5.33 as,

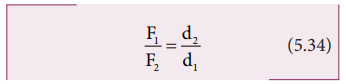
If F1 is the load and F2 is our effort, we get advantage when, d1< d2. This implies that F1> F2. Hence, we could lift a large load with small effort. The ratio (d2/d1) is called mechanical advantage of the simple lever. The pivoted point is called fulcrum.

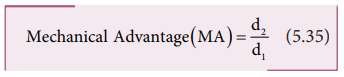
There are many simple machines that work on the above mentioned principle.