Kinetic Energy in Rotation

Kinetic Energy in Rotation

Let us consider a rigid body rotating with angular velocity ω about an axis as shown in Figure 5.30. Every particle of the body will have the same angular velocity ω and different tangential velocities v based on its positions from the axis of rotation.

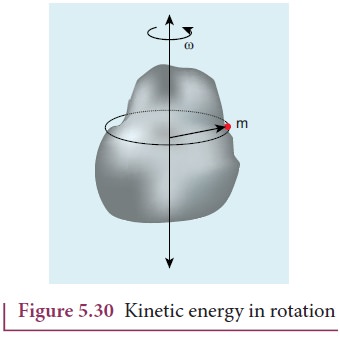
Let us choose a particle of mass mi situated at distance ri from the axis of rotation. It has a tangential velocity vi given by the relation, vi = ri ω. The kinetic energy KEi of the particle is,

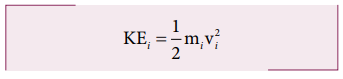
Writing the expression with the angular velocity,

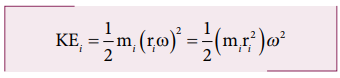
For the kinetic energy of the whole body, which is made up of large number of such particles, the equation is written with summation as,

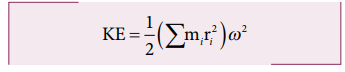
where, the term Σmi ri2 is the moment of inertia I of the whole body. I = Σmi ri2

Hence, the expression for KE of the rigid body in rotational motion is,

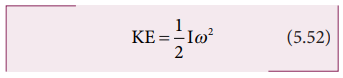
This is analogous to the expression for kinetic energy in translational motion.

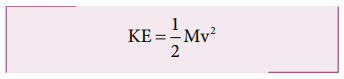
Relation between rotational kinetic energy and angular momentum

Let a rigid body of moment of inertia I rotate with angular velocity ω.

The angular momentum of a rigid body is, L = I ω

The rotational kinetic energy of the rigid body is, KE = 1/2 Iω2

By multiplying the numerator and denominator of the above equation with I, we get a relation between L and KE as,