Chapter: 11th Physics : UNIT 5 : Motion of System of Particles and Rigid Bodies
Solved Example Problems for Physics: Motion of System of Particles and Rigid Bodies
Numerical Problems
1. A uniform disc of mass 100g has a diameter of 10 cm. Calculate the total energy of the disc when rolling along a horizontal table with a velocity of 20 cms-1. (take the surface of table as reference)
Answer
Mass of the disc m = 100 g = 0.1 kg.
Diameter of the disc d = 10 cm
Radius of the disc r =
5 cm = 0.05m
Rolling with a velocity
v = 20 cms-1 = 0.20 ms-1
Total energy of the
disc ETot = ?
ETot =
Translational K.E. + rotational K.E.
Moment of inertia (M.I)
of the disc about its own axis

Ans: 0.1028 J
2. A particle of mass 5 units is moving with a uniform speed of v = 3√2 units in the XOY plane along the line y = x + 4. Find the magnitude of angular momentum.
Answer
Equation of line x - y
+ 4 = 0
Mass of particle = 5
units
Speed v - 3 √2 units
Distance of line from
origin r =
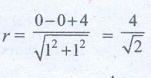
Angel momentum L = mvr = 5 × 3 √2 × 4/√2 = 60 units
Ans: 60 units
3. A fly wheel rotates with a uniform angular acceleration. If its angular velocity increases from 20π rad/s to 40π rad/s in 10 seconds. Find the number of rotations in that period.
Answer:
Initial Angular
Velocity ω0 = 20π rad s-1
Final Angular velocity ω
= 40 π rad s-1
time taken, t = 10 s
No. of rotations / s =
?

= 150 rotations.
Ans: 150 rotations
4. A uniform rod of mass m and length l makes a constant angle θ with an axis of rotation which passes through one end of the rod. Find the moment of inertia about this axis.
Answer
θ - angle that rod
makes with the axis (vertical)
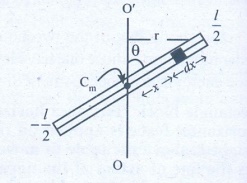
Linear mass density λ =
m/l
Consider dx. the part of rod
Mass dx, the part of
rod dm=λ.dx
dm= m/l dx. The M.I of the rod about OO'
I = ∫ r2 dm
Where is the
perpendicular distance from the elementary mass dm.
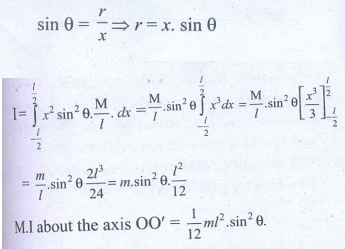
M.I about the axis OO'
= 1/12 ml2.sin2
θ.
Ans: 1/12 Ml 2 sin2 θ
5. Two particles P and Q of mass 1kg and 3 kg respectively start moving towards each other from rest under mutual attraction. What is the velocity of their center of mass?
Answer
Mass of particle P m1 = 1 kg.
Mass of particle Q m2 = 3 kg
Velocity of particle P
= velocity of particle Q
but in opposite
direction.
velocity of center of
mass vcm = ?
Ans: Zero
6. Find the moment of inertia of a hydrogen molecule about an axis passing through its center of mass and perpendicular to the inter-atomic axis. Given: mass of hydrogen atom 1.7 × 10-27 kg and inter atomic distance is equal to 4 × 10-10 m.
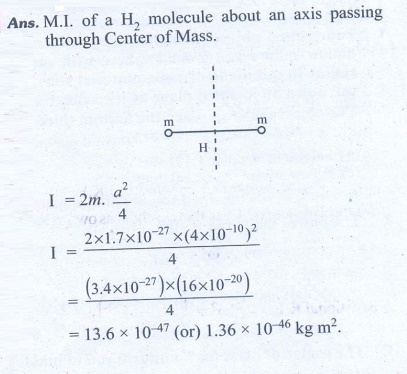
Ans: 1.36 × 10-46 kg m2
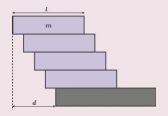
7. On the edge of a wall, we build a brick tower that only holds because of the bricks’ own weight. Our goal is to build a stable tower whose overhang d is greater than the length l of a single brick. What is the minimum number of bricks you need?
(Hint: Find the center of mass for each brick and add.)
8. The 747 boing plane is landing at a speed of 70m s-1. Before touching the ground, the wheels are not rotating. How long a skid mark do the wing wheels leave (assume their mass is 100 kg which is distributed uniformly, radius is 0.7 m, and the coefficient of friction with the ground is 0.5)?
Ans: 2.1 m
Conceptual Questions
1. When a tree is cut, the cut is made on the side facing the direction in which the tree is required to fall. Why?
Answer:
The
weight of tree exerts a torque about the point where the cut is made. This
causes rotation of the tree about the cut.
2. Why does a porter bend forward while carrying a sack of rice on his back?
Answer:
A
porter bends forward while carrying a sack of rice on his back because to
change the position of centre of gravity such that he gets the stability.
3. Why is it much easier to balance a meter scale on your finger tip than balancing on a match stick?
Answer
Meter
scale is longer and larger than a match stick. Meter scale’s Centre of gravity
is higher but match stick has Centre of gravity much lower as compared to
scale. Higher the centre of gravity easier it is to balance.
4. Two identical water bottles one empty and the other filled with water are allowed to roll down an inclined plane. Which one of them reaches the bottom first? Explain your answer.
Answer
Water filled bottle. Because the moment of inertia of the empty bottle is higher than the moment of inertia of the water filled bottle.
5. Write the relation between angular momentum and rotational kinetic energy. Draw a graph for the same. For two objects of same angular momentum, compare the moment of inertia using the graph.
Answer:
Angular
momentum, L = Iω.
Rotational
K.E., EK = 1/2 Iω2
Multiply
by 21 both sides (21) EK = —— 2IEk = (Ico)2
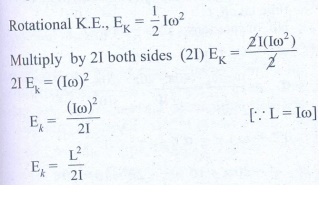
Where,
L is the angular momentum and I is the moment of inertia.
Graph
between KE and L :

The
graph shows that of the two bodies of same angular momentum, those one have
less rotational kinetic energy has higher moment of inertia.
6. A rectangle block rests on a horizontal table. A horizontal force is applied on the block at a height h above the table to move the block. Does the line of action of the normal force N exerted by the table on the block depend on h?
Answer
(i) Yes. The line of
action of the normal force N exerted by the table on the block depend on h.
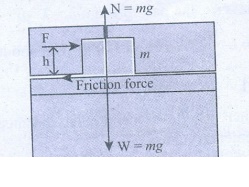
(ii) When height of the
applied force ‘h’ increases, a torque
is produced by the applied force and frictional force such that block start to
tilt.
(iii) To balance this
effect, line of action of normal force shift away’from applied force and make a
opposite torque, joining with gravitational force ‘W’.
7. Three identical solid spheres move down through three inclined planes A, B and C all same dimensions. A is without friction, B is undergoing pure rolling and C is rolling with slipping. Compare the kinetic energies EA, EB and EC at the bottom.
Answer
(i) In this case, when
three identical solid spheres starts to move on the inclined planes, they all
have same potential energy.
(ii) During the motion,
the potential energy is converted into kinetic energy.
(iii) According to law
of conservation of energy, at the bottom all the potential energy is converted
into kinetic energy.
(iv) Such that all
three spheres have same kinetic energy at the bottom whatever be the type of
motion, i.e. EA = EB = Ec.
8. Give an example to show that the following statement is false. ‘any two forces acting on a body can be combined into single force that would have same effect’.
Answer
(i) Consider two equal
and opposite forces acting on a wheel.
(ii) If two forces
combined and acting on single point on the wheel, there will be no effect.
However, if they act separately on the edges of the wheel, there will be a
rotating effect.
(iii) This example
falsifies the given statement.
SOLVED EXAMPLE
1. Three particles of masses m1 = 1 kg, m2 = 2 kg and m3 = 3 kg are placed at the corners of an equilateral triangle of side 1m as shown in Figure. Find the position of center of mass.
Solution:
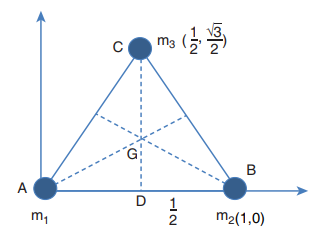
The center of mass of an equilateral triangle lies at its geometrical center G.
The positions of the mass m1, m2 and m3 are at positions A, B and C as shown in the Figure.
From the given position of the masses, the coordinates of the masses m1 and m2 are easily marked as (0,0) and (1,0) respectively.
To find the position of m3 the Pythagoras theorem is applied. As the ∆DBC is a right angle triangle,
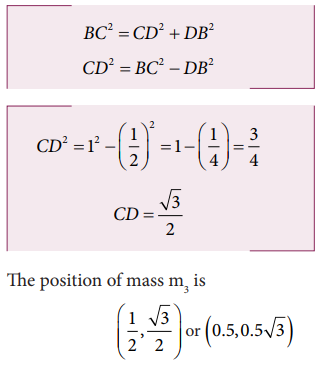

2. An electron of mass 9 ×10 -31 kg revolves around a nucleus in a circular orbit of radius 0.53 Å. What is the angular momentum of the electron? (Velocity of electron is, v = 2.2 ×106 m s -1 )
Solution:
Mass of the electron, m = 9 × 10−31 kg
Radius of the electron, r = 0.53 Å = 0.53 x 10-10m
Velocity of the electron, v = 2.2 × 106 ms-1
Angular momentum of electron is, L = I ω
Electron is considered as a point mass. Hence, its moment of inertia is, I = m r2
The relation, ω = v/r could be used.
Angular momentum, L = mr2 × v/r
= mvr
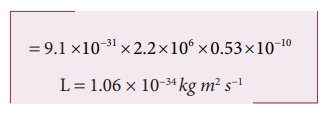
3. A solid sphere of mass 20 kg and radius 0.25 m rotates about an axis passing through the center. What is the angular momentum if the angular velocity is 5 rad s-1
Solution:
Mass of the sphere, m = 20 kg
Radius r = 0.25 m
Angular velocity ω = 5 rad s-1
Solution:
Angular momentum L = Iω = 2/5 mr2ω
=2/5 x 20 (.25)2 x 5
L = 2.5 kg m2s-1
4. A solid cylinder when dropped from a height of 2 m acquires a velocity while reaching the ground. If the same cylinder is rolled down from the top of an inclined plane to reach the ground with same velocity, what must be the height of the inclined plane? Also compute the velocity.
Solution:

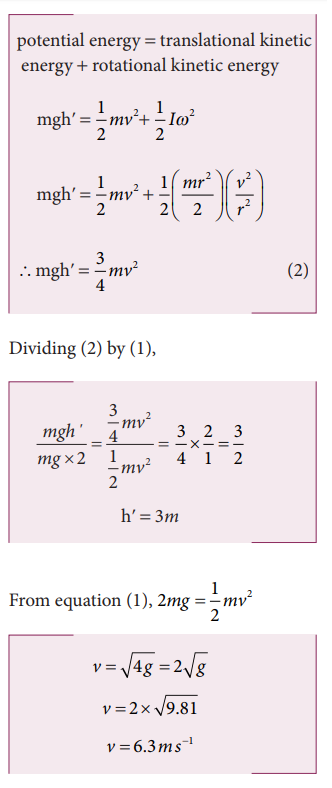
5. A small particle of mass m is projected with an initial velocity v at an angle θ with x axis in X-Y plane as shown in Figure. Find the angular momentum of the particle.
Solution:
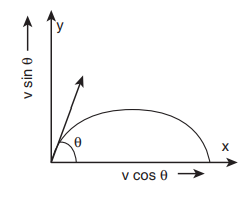
Let the particle of mass m cross a horizontal distance x in time t.

6. From a complete ring of mass M and radius R, a sector angle θ is removed. What is the moment of inertia of the incomplete ring about axis passing through the center of the ring and perpendicular to the plane of the ring?
Solution:
Let R be the radius of the ring and M be the total mass of the complete ring.
Let m be the mass of the section removed from the ring then, mass of the incomplete ring is M-m

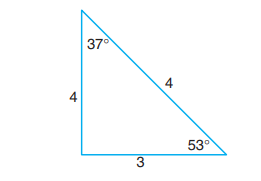
7. A massless right tangled triangle is suspended with its right angle corner. A mass of 100 kg is suspended from another corner B which subtends an angle 53o. Find the mass m that should be suspended from other corner C so that BC (hypotenuse) remains horizontal.
Solution:

Where, x1 and x2 are the arm lengths.
The right angle triangle with angles 37o, 53o and 90o is a special triangle which has the respective sides in the ratio, 3:4:5 as shown in the diagram.
Substituting the values in equation (1),
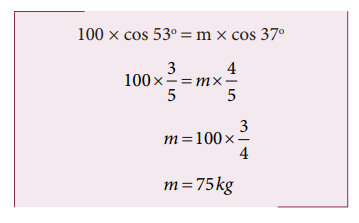
8. If energy of 1000 J is spent in increasing the speed of a flywheel from 30 rpm to 720 rpm, find the moment of inertia of the wheel.
Solution:

9. Consider two cylinders with same radius and same mass. Let one of the cylinders be solid and another one be hollow. When subjected to same torque, which one among them gets more angular acceleration than the other?
Solution:
Moment of inertia of a solid cylinder
Moment of inertia of a hollow cylinder about its axis I h = MR2
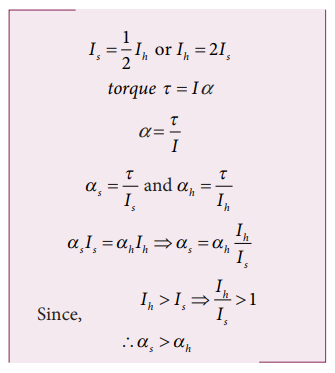
For the same torque, a solid cylinder gets more acceleration than a hollow cylinder.
10. A thin horizontal circular disc is rotating about a vertical axis passing through its center. An insect goes from A to point B along its diameter as shown in Figure. Discuss how the angular speed of the circular disc changes?
Solution:
As the disc is freely rotating, with the insect on it, the angular momentum of the system is conserved.
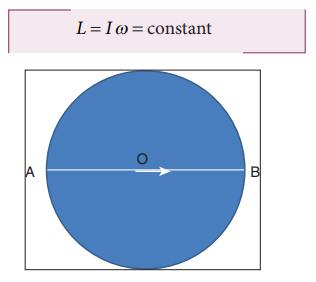
When the insect moves towards the center (from A to O), the moment of inertia (I) increases. Thus, the angular velocity (ω) increases. When it moves away from center (from O to B), the moment of inertia (I) decreases. Thus, the angular velocity (ω) decreases.
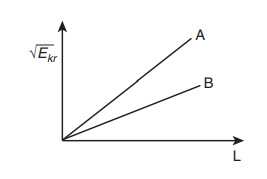
11. (i) What is the shape of the graph between √Ekr and L? (Ekr is the rotational kinetic energy and L is angular momentum)
(ii) What information can you get from the slope of the graph?
(iii) You are given the graph of √Ekr and L for two bodies A and B. Which one has more moment of inertia?
Solution:
i) We know that, Rotational kinetic Energy

The shape of the graph is a straight line
ii) The slope of the graph gives the value of moment of inertia I.
iii) We know that the slope gives the value of moment of Inertia. The line A has higher slope and hence more moment of Inertia.
12. Consider a thin uniform circular ring rolling down in an inclined plane without slipping. Compute the linear acceleration along the inclined plane if the angle of inclination is 45˚.
Solution:
The linear acceleration along the inclined plane can be computed by
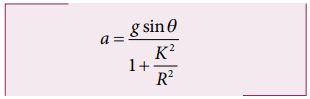
For a thin uniform circular ring, axis passing through its center is I = MR2

Solved Example Problems for Center of Mass of Two Point Masses
Example 5.1
Two point masses 3 kg and 5 kg are at 4 m and 8 m from the origin on X-axis. Locate the position of center of mass of the two point masses (i) from the origin and (ii) from 3 kg mass.
Solution
Let us take, m1 = 3 kg and m2= 5 kg
(i) To find center of mass from the origin:
The point masses are at positions, x1 = 4 m, x2 = 8 m from the origin along X axis.
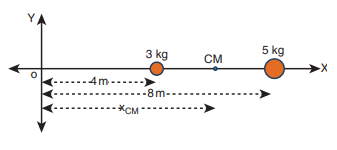
The center of mass xCM can be obtained using equation 5.4.

The center of mass is located 6.5 m from the origin on X-axis.
(ii) To find the center of mass from 3 kg mass:
The origin is shifted to 3 kg mass along X-axis. The position of 3 kg point mass is zero (x1 = 0) and the position of 5 kg point mass is 4 m from the shifted origin (x2 = 4 m).
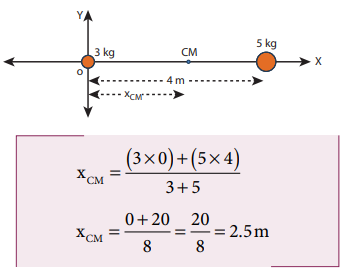
The center of mass is located 2.5 m from 3 kg point mass, (and 1.5 m from the 5 kg point mass) on X-axis.
This result shows that the center of mass is located closer to larger mass.
If the origin is shifted to the center of mass, then the principle of moments holds good.
m1x1=m2x2; 3x2.5=5x1.5;7.5=7.5
When we compare case (i) with case (ii), the xCM = 2.5m from 3 kg mass could also be obtained by subtracting 4 m (the position of 3 kg mass) from 6.5 m, where the center of mass was located in case (i)
Example 5.2
From a uniform disc of radius R, a small disc of radius R/2 is cut and removed as shown in the diagram. Find the center of mass of the remaining portion of the disc.
Solution
Let us consider the mass of the uncut full disc be M. Its center of mass would be at the geometric center of the disc on which the origin coincides.
Let the mass of the small disc cut and removed be m and its center of mass is at a position R/2 to the right of the origin as shown in the figure.
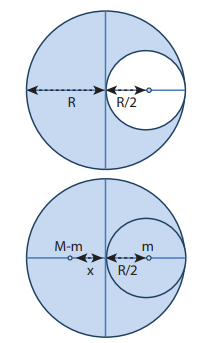
Hence, the remaining portion of the disc should have its center of mass to the left of the origin; say, at a distance x. We can write from the principle of moments,
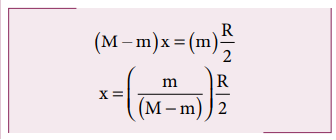
If σ is the surface mass density (i.e. mass per unit surface area), σ=M/πR2; then, the mass m of small disc is,

The center of mass of the remaining portion is at a distance R/6 to the left from the center of the disc.
If, the small disc is removed concentrically from the large disc, what will be the position of the center of mass of the remaining portion of disc?
Example 5.3

Solved Example Problems for Center of mass for uniform distribution of mass
Example 5.4
Locate the center of mass of a uniform rod of mass M and length l.
Solution
Consider a uniform rod of mass M and length whose one end coincides with the origin as shown in Figure. The rod is kept along the x axis. To find the center of mass
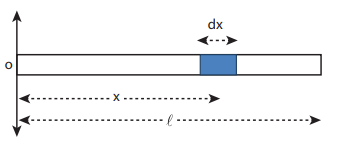
of this rod, we choose an infinitesimally small mass dm of elemental length dx at a distance x from the origin.
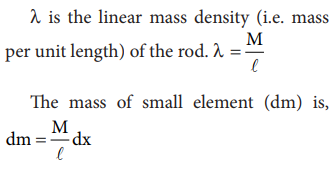
Now, we can write the center of mass equation for this mass distribution as,
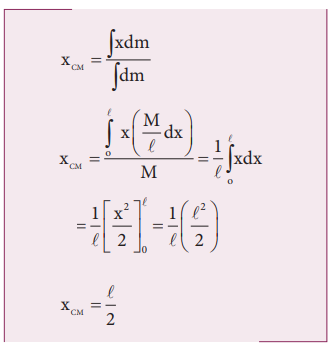
As the position l/2 is the geometric center of the rod, it is concluded that the center of mass of the uniform rod is located at its geometric center itself.
Solved Example Problems for Motion of Center of Mass
Example 5.5
A man of mass 50 kg is standing at one end of a boat of mass 300 kg floating on still water. He walks towards the other end of the boat with a constant velocity of 2 ms-1 with respect to a stationary observer on land. What will be the velocity of the boat, (a) with respect to the stationary observer on land? (b) with respect to the man walking in the boat?
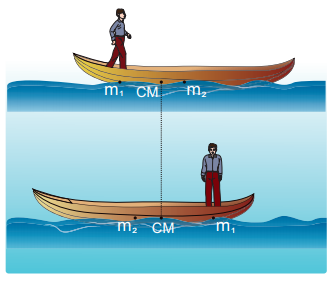
[Given: There is friction between the man and the boat and no friction between the boat and water.]
Solution
Mass of the man (m1) is, m1= 50 kg
Mass of the boat (m2) is, m2 = 300 kg
With respect to a stationary observer:
The man moves with a velocity, v1 = 2 m s-1 and the boat moves with a velocity v2 (which is to be found)
(i) To determine the velocity of the boat with respect to a stationary observer on land:
As there is no external force acting on the system, the man and boat move due to the friction, which is an internal force in the boat-man system. Hence, the velocity of the center of mass is zero (vCM = 0).
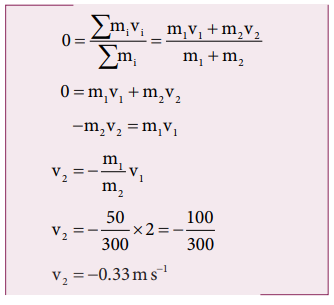
The negative sign in the answer implies that the boat moves in a direction opposite to that of the walking man on the boat to a stationary observer on land.
(ii) To determine the velocity of the boat with respect to the walking man:
We can find the relative velocity as,
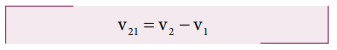
where, v21 is the relative velocity of the boat with respect to the walking man.
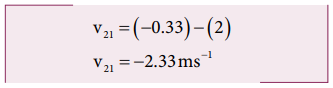
The negative sign in the answer implies that the boat appears to move in the opposite direction to the man walking in the boat.
The magnitude of the relative velocity of the boat with respect to the walking man is greater than the magnitude of the relative velocity of the boat with respect to the stationary observer.
The negative signs in the two answers indicate the opposite direction of the boat with respect to the stationary observer and the walking man on the boat.
Example 5.6
A projectile of mass 5 kg, in its course of motion explodes on its own into two fragments. One fragment of mass 3 kg falls at three fourth of the range R of the projectile. Where will the other fragment fall?
Solution
It is an explosion of its own without any external influence. After the explosion, the center of mass of the projectile will continue to complete the parabolic path even though the fragments are not following the same parabolic path. After the fragments have fallen on the ground, the center of mass rests at a distance R (the range) from the point of projection as shown in the diagram.
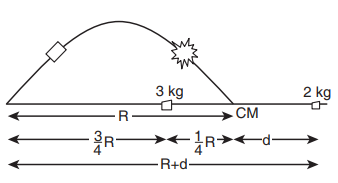
If the origin is fixed to the final position of the center of mass, the principle of moments holds good.

The other fragment falls at a distance of 1.375R from the point of launching. (Here R is the range of the projectile.)
Solved Example Problems for Torque
Example 5.7
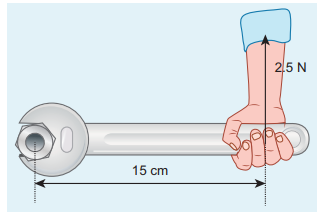
If the force applied is perpendicular to the handle of the spanner as shown in the diagram, find the (i) torque exerted by the force about the center of the nut, (ii) direction of torque and (iii) type of rotation caused by the torque about the nut.
Solution
Arm length of the spanner, r = 15 cm = = 15×10−2m
Force, F = 2.5 N
Angle between r and F, θ = 90o
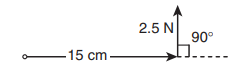
(i) Torque, τ θ = rF sin
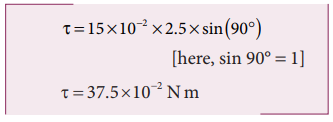
(ii) As per the right hand rule, the direction of torque is out of the page.
(iii) The type of rotation caused by the torque is anticlockwise.
Example 5.8

Example 5.9
A crane has an arm length of 20 m inclined at 30o with the vertical. It carries a container of mass of 2 ton suspended from the top end of the arm. Find the torque produced by the gravitational force on the container about the point where the arm is fixed to the crane. [Given: 1 ton = 1000 kg; neglect the weight of the arm. g = 10 ms-2]
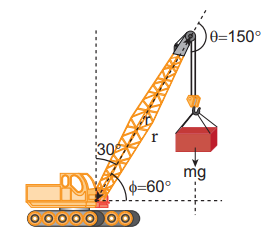
Solution
The force F at the point of suspension is due to the weight of the hanging mass.
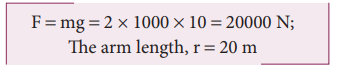
We can solve this problem by three different methods.
Method – I
The angle (θ) between the arm length (r) and the force (F) is, θ = 150o
The torque (τ) about the fixed point of the arm is,
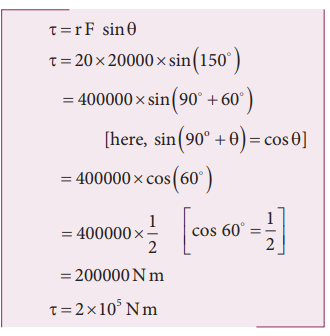
Method – II
Let us take the force and perpendicular distance from the point where the arm is fixed to the crane.
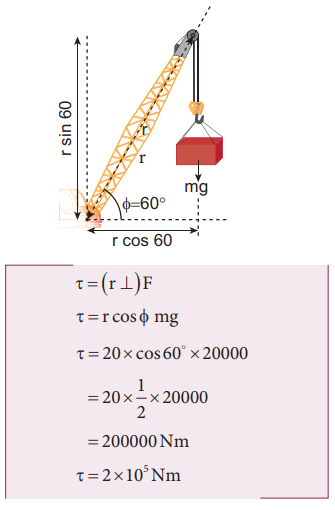
Method – III
Let us take the distance from the fixed point and perpendicular force.
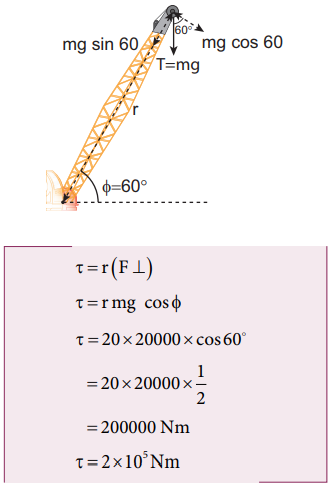
All the three methods, give the same answer
Solved Example Problems for Torque about an Axis
Example 5.10
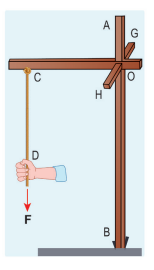
Three mutually perpendicular beams AB, OC, GH are fixed to form a structure which is fixed to the ground firmly as shown in the Figure. One string is tied to the point C and its free end D is pulled with a force F. Find the magnitude and direction of the torque produced by the force,
i. about the points D, C, O and B
ii. about the axes CD, OC, AB and GH.
Solution

The torque of a force about an axis is independent of the choice of the origin as long as it is chosen on that axis itself. Th is can be shown as below.
Let O be the origin on the axis AB, which is the rotational axis of a rigid body. F is the force acting at the point P. Now, choose another point O’ anywhere on the axis as shown in Figure 5.10.
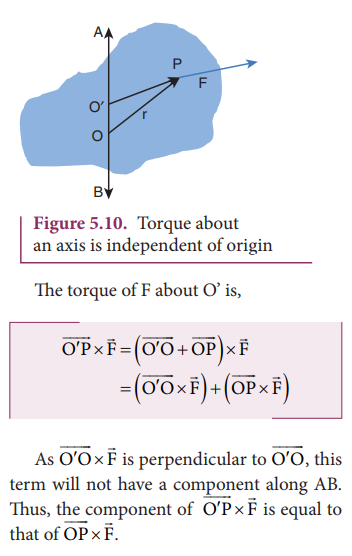
Solved Example Problems for Angular Momentum
Example 5.11
A particle of mass (m) is moving with constant velocity (v). Show that its angular momentum about any point remains constant throughout the motion.
Solution

The term ( OQsinθ ) is the perpendicular distance (d) between the origin and line along which the mass is moving. Hence, the angular momentum of the particle about the origin is,
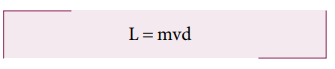
The above expression for angular momentum L, does not have the angle θ. As the momentum (p = mv) and the perpendicular distance (d) are constants, the angular momentum of the particle is also constant. Hence, the angular momentum is associated with bodies with linear motion also. If the straight path of the particle passes through the origin, then the angular momentum is zero, which is also a constant.
Solved Example Problems for Types of Equilibrium
Example 5.12
Arun and Babu carry a wooden log of mass 28 kg and length 10 m which has almost uniform thickness. They hold it at 1 m and 2 m from the ends respectively. Who will bear more weight of the log? [g = 10 ms-2]
Solution
Let us consider the log is in mechanical equilibrium. Hence, the net force and net torque on the log must be zero. The gravitational force acts at the center of mass of the log downwards. It is cancelled by the normal reaction forces RA and RB applied upwards by Arun and Babu at points A and B respectively. These reaction forces are the weights borne by them.
The total weight, W = mg = 28 × 10 = 280 N, has to be borne by them together. The reaction forces are the weights borne by each of them separately. Let us show all the forces acting on the log by drawing a free body diagram of the log.
For translational equilibrium:
The net force acting on the log must be zero.
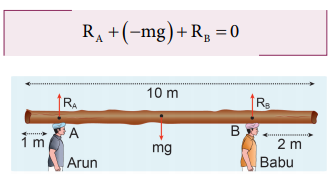
Here, the forces RA an RB are taken positive as they act upward. The gravitational force acting downward is taken negative.
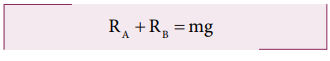
For rotational equilibrium:
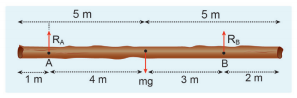
The net torque acting on the log must be zero. For ease of calculation, we can take the torque caused by all the forces about the point A on the log. The forces are perpendicular to the distances. Hence,
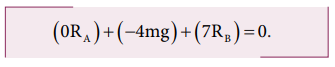
Here, the reaction force RA cannot produce any torque as the reaction forces pass through the point of reference A. The torque of force mg produces a clockwise turn about the point A which is taken negative and torque of force RB causes anticlockwise turn about A which is taken positive.

As RB is greater than RA, it is concluded that Babu bears more weight than Arun. The one closer to center of mass of the log bears more weight.
Solved Example Problems for Bending of Cyclist in Curves
Example 5.13
A cyclist while negotiating a circular path with speed 20 m s-1 is found to bend an angle by 30o with vertical. What is the radius of the circular path? (given, g = 10 m s-2)
Solution
Speed of the cyclist, v = 20 m s-1
Angle of bending with vertical, θ = 30o

Solved Example Problems for Moment of Inertia of a Uniform Rod
Example 5.14
Find the moment of inertia of a uniform rod about an axis which is perpendicular to the rod and touches any one end of the rod.
Solution
The concepts to form the integrand to find the moment of inertia could be borrowed from the earlier derivation. Now, the origin is fixed to the left end of the rod and the limits are to be taken from 0 to ℓ.
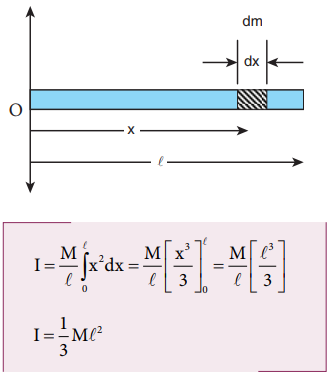
Solved Example Problems for Radius of Gyration
Example 5.15
Find the radius of gyration of a disc of mass M and radius R rotating about an axis passing through the center of mass and perpendicular to the plane of the disc.
Solution
The moment of inertia of a disc about an axis passing through the center of mass and perpendicular to the disc is,I = ½ MR2

From the case of a rod and also a disc, we can conclude that the radius of gyration of the rigid body is always a geometrical feature like length, breadth, radius or their combinations with a positive numerical value multiplied to it.
Solved Example Problems for Theorems of Moment of Inertia
Example 5.16
Find the moment of inertia of a disc of mass 3 kg and radius 50 cm about the following axes.
i. axis passing through the center and perpendicular to the plane of the disc,
ii. axis touching the edge and perpendicular to the plane of the disc and
iii. axis passing through the center and lying on the plane of the disc.
Solution
The mass, M = 3 kg, radius R = 50 cm = 50 × 10−2 m = 0.5 m
i. The moment of inertia (I) about an axis passing through the center and perpendicular to the plane of the disc is,
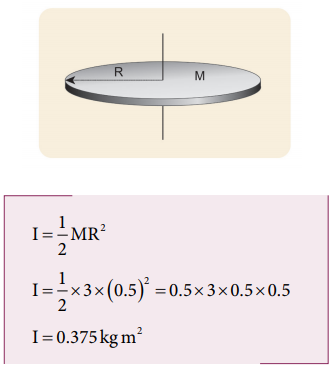
ii. The moment of inertia (I) about an axis touching the edge and perpendicular to the plane of the disc by parallel axis theorem is,
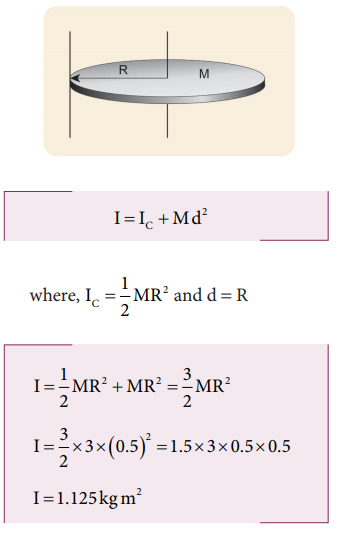
(iii) The moment of inertia (I) about an axis passing through the center and axis passing through the center and

About which of the above axis it is easier to rotate the disc?
It is easier to rotate the disc about an axis about which the moment of inertia is the least. Hence, it is case (iii).
Example 5.17
Find the moment of inertia about the geometric center of the given structure made up of one thin rod connecting two similar solid spheres as shown in Figure.

Solution
The structure is made up of three objects; one thin rod and two solid spheres.
The mass of the rod, M = 3 kg and the total length of the rod, ℓ = 80 cm = 0.8 m

The mass of the sphere, M = 5 kg and the radius of the sphere, R = 10 cm = 0.1 m

The moment of inertia of the sphere about geometric center of the structure is,
I sph = I C + Md2
Where, d = 40 cm + 10 cm = 50 cm = 0.5 m

As there are one rod and two similar solid spheres we can write the total moment of inertia (I) of the given geometric structure as, I = Irod + (2 × Isph )
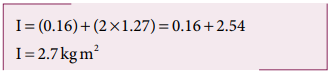
Solved Example Problems for Effect of Torque on Rigid Bodies
Example 5.18
A disc of mass 500 g and radius 10 cm can freely rotate about a fixed axis as shown in Figure A. light and inextensible string is wound several turns around it and 100 g body is suspended at its free end. Find the acceleration of this mass. [Given: The string makes the disc to rotate and does not slip over it. g = 10 m s-2.]
Solution

Let the mass of the disc be m1 and its radius R. The mass of the suspended body is m2.

As the light inextensible string is wound around the disc several times it makes the disc rotate without slipping over it. The translational acceleration of m2 and tangential acceleration of m1 will be the same. Let us draw the free body diagram (FBD) of m1 and m2 separately.
FBD of the disc:
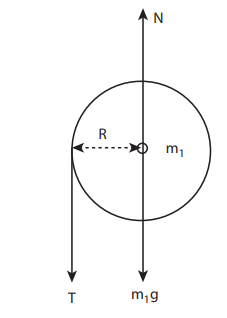
Its gravitational force (m1g) acts downward and normal force N exerted by the fixed support at the center acts upward. The tension T acts downward at the edge. The gravitational force (m1g) and the normal force (N) cancel each other. m1g = N
The tension T produces a torque (R T), which produces a rotational motion in the disc with angular acceleration, (α=a/R)
Here, a is the linear acceleration of a point at the edge of the disc. If the moment of inertia of the disc is I and its radius of gyration is K, then
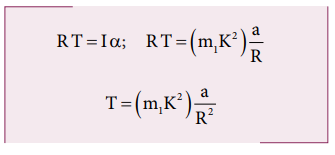
FBD of the body:
Its gravitational force (m2g) acts downward and the tension T acts upward. As (T < m2g), there is a resultant force (m2a) acting on it downward.
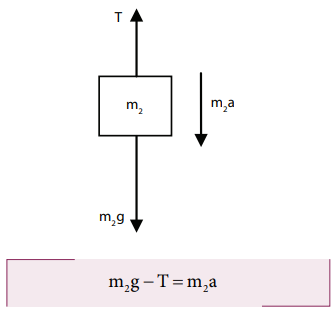
Substituting for T from the equation for disc,

Solved Example Problems for Conservation of Angular Momentum
Example 5.19
A jester in a circus is standing with his arms extended on a turn table rotating with angular velocity ω. He brings his arms closer to his body so that his moment of inertia is reduced to one third of the original value. Find his new angular velocity. [Given: There is no external torque on the turn table in the given situation.]
Solution
Let the moment of inertia of the jester with his arms extended be I. As there is no external torque acting on the jester and the turn table, his total angular momentum is conserved. We can write the equation,

The above result tells that the final angular velocity is three times that of initial angular velocity.
Solved Example Problems for Kinetic Energy in Rotation
Example 5.20
Find the rotational kinetic energy of a ring of mass 9 kg and radius 3 m rotating with 240 rpm about an axis passing through its center and perpendicular to its plane. (rpm is a unit of speen of rotation which means revolutions per minute)
Solution

Solved Example Problems for Slipping and Sliding(Rolling Motion)
Example 5.21
A rolling wheel has velocity of its center of mass as 5 m s-1. If its radius is 1.5 m and angular velocity is 3 rad s-1, then check whether it is in pure rolling or not.
Solution
Translational velocity (vTRANS) or velocity of center of mass, vCM = 5 m s-1
The radius is, R = 1.5 m and the angular velocity is, ω = 3 rad s-1
Rotational velocity, vROT = Rω
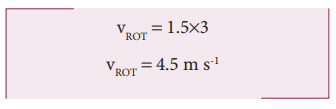
As vCM > Rω (or) vTRANS > Rω, It is not in pure rolling, but sliding.
Solved Example Problems for Kinetic Energy in Pure Rolling(Rolling Motion)
Example 5.22
A solid sphere is undergoing pure rolling. What is the ratio of its translational kinetic energy to rotational kinetic energy?
Solution
The expression for total kinetic energy in pure rolling is,
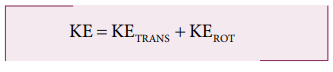
For any object the total kinetic energy as per equation 5.58 and 5.59 is,
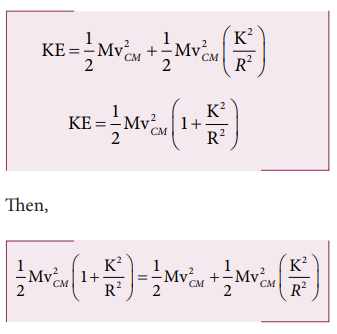
The above equation suggests that in pure rolling the ratio of total kinetic energy, translational kinetic energy and rotational kinetic energy is given as,

Solved Example Problems for Rolling on Inclined Plane(Rolling Motion)
Example 5.23
Four round objects namely a ring, a disc, a hollow sphere and a solid sphere with same radius R start to roll down an incline at the same time. Find out which object will reach the bottom first.
Solution
For all the four objects namely the ring, disc, hollow sphere and solid sphere, the radii of gyration K are R,
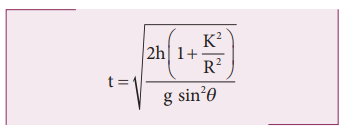
The one with least value of radius of gyration K will take the shortest time to reach the bottom of the inclined plane. The order of objects reaching the bottom is first, solid sphere; second, disc; third, hollow sphere and last, ring.
Related Topics