Chapter: 11th Physics : UNIT 5 : Motion of System of Particles and Rigid Bodies
Theorems of Moment of Inertia
Theorems of Moment of Inertia
As the moment of inertia depends on the axis of rotation and also the orientation of the body about that axis, it is different for the same body with different axes of rotation. We have two important theorems to handle the case of shifting the axis of rotation.
(i) Parallel axis theorem:
Parallel axis theorem states that the moment of inertia of a body about any axis is equal to the sum of its moment of inertia about a parallel axis through its center of mass and the product of the mass of the body and the square of the perpendicular distance between the two axes.
If IC is the moment of inertia of the body of mass M about an axis passing through the center of mass, then the moment of inertia I about a parallel axis at a distance d from it is given by the relation,
I = IC + Md2 (5.46)
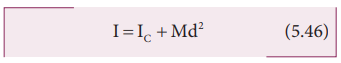
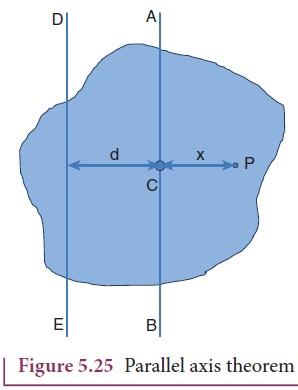
Let us consider a rigid body as shown in Figure 5.25. Its moment of inertia about an axis AB passing through the center of mass is IC. DE is another axis parallel to AB at a perpendicular distance d from AB. The moment of inertia of the body about DE is I. We attempt to get an expression for I in terms of IC. For this, let us consider a point mass m on the body at position x from its center of mass.
The moment of inertia of the point mass about the axis DE is, m( x + d)2.
The moment of inertia I of the whole body about DE is the summation of the above expression.
I = + ∑ m (x+d)2
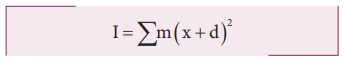
This equation could further be written as,

Here, ∑mx2 is the moment of inertia of the body about the center of mass. Hence, IC = ∑mx2
The term, ∑mx = 0 because, x can take positive and negative values with respect to the axis AB. The summation ( ∑mx) will be zero.
Thus, I = IC + ∑md2 = IC + ( ∑m)d2
Here, Σm is the entire mass M of the object ( ∑m = M )
I = IC + Md2
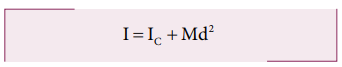
Hence, the parallel axis theorem is proved.
(ii) Perpendicular axis theorem:
This perpendicular axis theorem holds good only for plane laminar objects.
The theorem states that the moment of inertia of a plane laminar body about an axis perpendicular to its plane is equal to the sum of moments of inertia about two perpendicular axes lying in the plane of the body such that all the three axes are mutually perpendicular and have a common point.
Let the X and Y-axes lie in the plane and Z-axis perpendicular to the plane of the laminar object. If the moments of inertia of the body about X and Y-axes are IX and IY respectively and IZ is the moment of inertia about Z-axis, then the perpendicular axis theorem could be expressed as,
IZ =IX +IY (5.47)
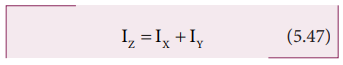
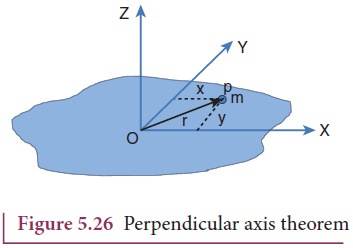
To prove this theorem, let us consider a plane laminar object of negligible thickness on which lies the origin (O). The X and Y-axes lie on the plane and Z-axis is perpendicular to it as shown in Figure 5.26. The lamina is considered to be made up of a large number of particles of mass m. Let us choose one such particle at a point P which has coordinates (x, y) at a distance r from O.
The moment of inertia of the particle about Z-axis is, mr2
The summation of the above expression gives the moment of inertia of the entire lamina about Z-axis as, IZ = ∑mr2
Here, r2 = x2 + y2
Then, IZ = ∑m ( x2 + y2 )
IZ = ∑m x2 + ∑m y2
IZ = ∑m x2 + ∑m y2
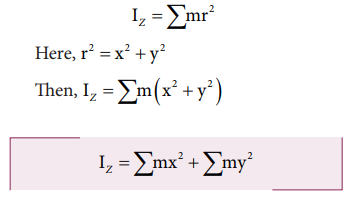
In the above expression, the term Σmx 2 is the moment of inertia of the body about the Y-axis and similarly the term Σmy2 is the moment of inertia about X-axis. Thus,
IX =∑my2
and
IY =∑mx2

Substituting in the equation for Iz gives,
IZ = IX + IY
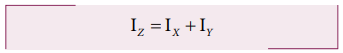
Thus, the perpendicular axis theorem is proved.
Solved Example Problems for Theorems of Moment of Inertia
Example 5.16
Find the moment of inertia of a disc of mass 3 kg and radius 50 cm about the following axes.
i. axis passing through the center and perpendicular to the plane of the disc,
ii. axis touching the edge and perpendicular to the plane of the disc and
iii. axis passing through the center and lying on the plane of the disc.
Solution
The mass, M = 3 kg, radius R = 50 cm = 50 × 10−2 m = 0.5 m
i. The moment of inertia (I) about an axis passing through the center and perpendicular to the plane of the disc is,
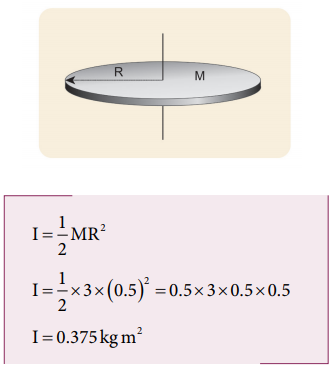
ii. The moment of inertia (I) about an axis touching the edge and perpendicular to the plane of the disc by parallel axis theorem is,
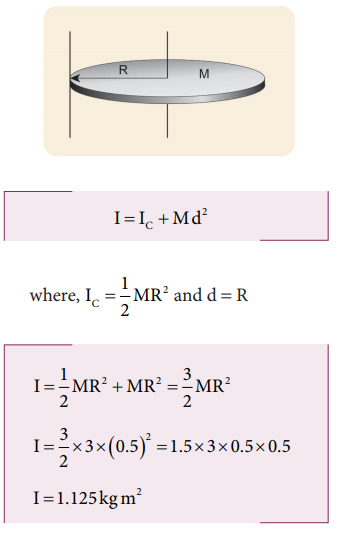
(iii) The moment of inertia (I) about an axis passing through the center and axis passing through the center and

About which of the above axis it is easier to rotate the disc?
It is easier to rotate the disc about an axis about which the moment of inertia is the least. Hence, it is case (iii).
Example 5.17
Find the moment of inertia about the geometric center of the given structure made up of one thin rod connecting two similar solid spheres as shown in Figure.

Solution
The structure is made up of three objects; one thin rod and two solid spheres.
The mass of the rod, M = 3 kg and the total length of the rod, ℓ = 80 cm = 0.8 m

The mass of the sphere, M = 5 kg and the radius of the sphere, R = 10 cm = 0.1 m

The moment of inertia of the sphere about geometric center of the structure is,
I sph = I C + Md2
Where, d = 40 cm + 10 cm = 50 cm = 0.5 m

As there are one rod and two similar solid spheres we can write the total moment of inertia (I) of the given geometric structure as, I = Irod + (2 × Isph )
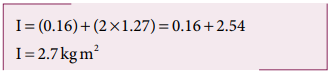
Related Topics