Radius of Gyration

Radius of Gyration

For bulk objects of regular shape with uniform mass distribution, the expression for moment of inertia about an axis involves their total mass and geometrical features like radius, length, breadth, which take care of the shape and the size of the objects. But, we need an expression for the moment of inertia which could take care of not only the mass, shape and size of objects, but also its orientation to the axis of rotation. Such an expression should be general so that it is applicable even for objects of irregular shape and non-uniform distribution of mass. The general expression for moment of inertia is given as,

I=MK2          (5.44)

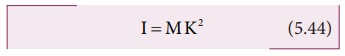
where, M is the total mass of the object and K is called the radius of gyration,

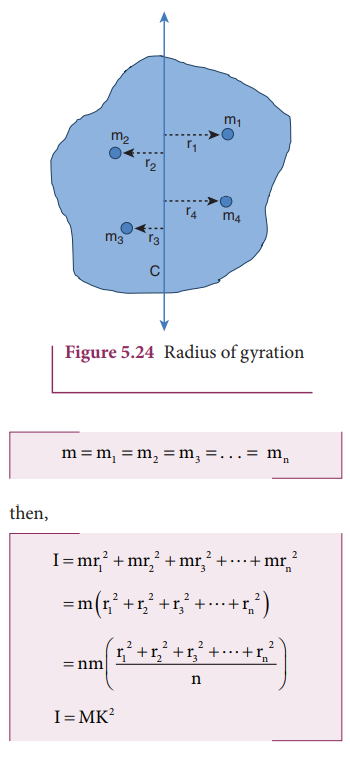
The radius of gyration of an object is the perpendicular distance from the axis of rotation to an equivalent point mass, which would have the same mass as well as the same moment of inertia of the object.

As the radius of gyration is distance, its unit is m. Its dimension is L.

A rotating rigid body with respect to any axis, is considered to be made up of point masses m1, m2, m3, . . .mn at perpendicular distances (or positions) r1, r2, r3 . . . rn respectively as shown in Figure 5.24.

The moment of inertia of that object can be written as,

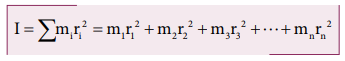
If we take all the n number of individual masses to be equal,

where, nm is the total mass M of the body and K is the radius of gyration.

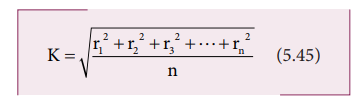
The expression for radius of gyration indicates that it is the root mean square (rms) distance of the particles of the body from the axis of rotation.

In fact, the moment of inertia of any object could be expressed in the form, I = MK2.

For example, let us take the moment of inertia of a uniform rod of mass M and length l. Its moment of inertia with respect to a perpendicular axis passing through the center of mass is, I= (1/12) Ml2

Solved Example Problems for Radius of Gyration

Example 5.15

Find the radius of gyration of a disc of mass M and radius R rotating about an axis passing through the center of mass and perpendicular to the plane of the disc.

Solution

The moment of inertia of a disc about an axis passing through the center of mass and perpendicular to the disc is,I = ½ MR2

From the case of a rod and also a disc, we can conclude that the radius of gyration of the rigid body is always a geometrical feature like length, breadth, radius or their combinations with a positive numerical value multiplied to it.