Chapter: 11th Physics : UNIT 8 : Heat and Thermodynamics
Solved Example Problems for Thermodynamic Processes
Isothermal process
EXAMPLE 8.16
A 0.5 mole of gas at temperature 300 K expands isothermally from an initial volume of 2 L to 6 L
(a) What is the work done by the gas?
(b) Estimate the heat added to the gas?
(c) What is the final pressure of the gas? (The value of gas constant, R = 8.31 J mol-1 K-1)
Solution
(a) We know that work done by the gas in an isothermal expansion
Since ┬Ą = 0.5
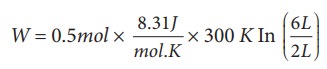
W = 1.369 kJ
Note that W is positive since the work is done by the gas.
(b) From the First law of thermodynamics, in an isothermal process the heat supplied is spent to do work.
Therefore, Q = W = 1.369 kJ. Thus Q is also positive which implies that heat flows in to the system.
(c) For an isothermal process
PiVi = PfVf = ┬ĄRT
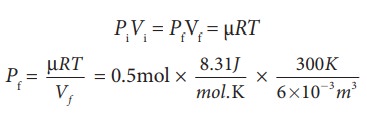
=207.75 k Pa
EXAMPLE 8.17
The following PV curve shows two isothermal processes for two different temperatures and. Identify the higher temperature of these two.
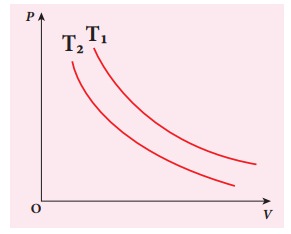
Solution
To determine the curve corresponding to higher temperature, draw a horizontal line parallel to x axis as shown in the figure. This is the constant pressure line. The volumes V1 and V2 belong to same pressure as the vertical lines from V1 and V2 meet the constant pressure line.
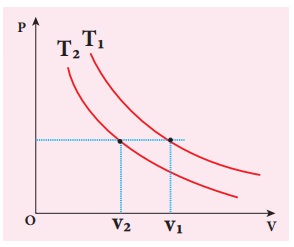
At constant pressure, higher the volume of the gas, higher will be the temperature. From the figure, as V1 > V2 we conclude T1 > T2. In general the isothermal curve closer to the origin, has lower temperature.
Adiabatic process
EXAMPLE 8.18

We often have the experience of pumping air into bicycle tyre using hand pump. Consider the air inside the pump as a thermodynamic system having volume V at atmospheric pressure and room temperature, 27┬░C. Assume that the nozzle of the tyre is blocked and you push the pump to a volume 1/4 of V. Calculate the final temperature of air in the pump? (For air , since the nozzle is blocked air will not flow into tyre and it can be treated as an adiabatic compression).
Solution
Here, the process is adiabatic compression. The volume is given and temperature is to be found. we can use the equation (8.38 )
TiVi╬│-1 = TfVf╬│-1.
Ti = 300 K (273+27┬░C = 300 K)
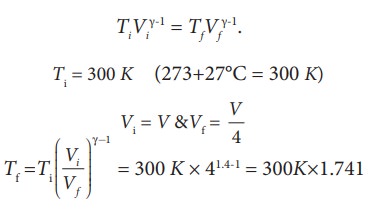
T2 Ōēł 522 K or 2490C
This temperature is higher than the boiling point of water. So it is very dangerous to touch the nozzle of blocked pump when you pump air.
EXAMPLE 8.19
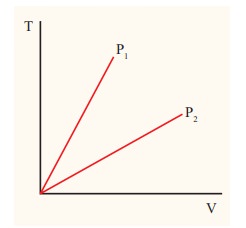
The following graph shows a V-T graph for isobaric processes at two different pressures. Identify which one occurs at higher pressure.
Solution
From the ideal gas equation,
V = (┬ĄR/P)T
V-T graph is a straight line passing the origin.
The slope = ┬ĄR/P
The slope of V-T graph is inversely proportional to the pressure. If the slope is greater, lower is the pressure.
Here P1 has larger slope than P2. So P2 > P1.
Suppose the graph is drawn between T and V (Temperature along the x-axis and Volume along the y-axis) then will we still have P2 > P1?
EXAMPLE 8.20
One mole of an ideal gas initially kept in a cylinder at pressure 1 MPa and temperature 27┬░C is made to expand until its volume is doubled.
(a)ŌĆé How much work is done if the expansion is (i) adiabatic (ii) isobaric (iii) isothermal?
(b) Identify the processes in which change in internal energy is least and is maximum.
(c) Show each process on a PV diagram.
(d) Name the processes in which the heat
(Take ╬│ = 5/3 and R=8.3 J mol-1 K-1)
Solution
(a) (i) In an adiabatic process the work done by the system is
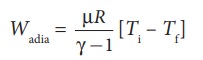
To find the final temperature Tf, we can use adiabatic equation of state.

(ii) In an isobaric process the work done by the system
W = P ŌłåV = P(Vf ŌĆō Vi)
and Vf = 2Vi so W = 2PVi
To find Vi, we can use the ideal gas law for initial state. PiVi = RTi
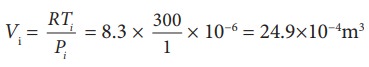
The work done during isobaric process,
W = 2 ├Ś 106 ├Ś 24.9 ├Ś 10ŌłÆ4 = 4.9 kJ
(iii) In an isothermal process the work done by the system,
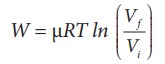
In an isothermal process the initial room temperature is constant.
W = 1 ├Ś 8.3 ├Ś 300 ├Ś ln(2) = 1.7kJ
(b) Comparing all three processes, we see that the work done in the isobaric process is the greatest, and work done in the adiabatic process is the least.
![]()
![]() (c) The PV diagram is shown in the Figure.
(c) The PV diagram is shown in the Figure.
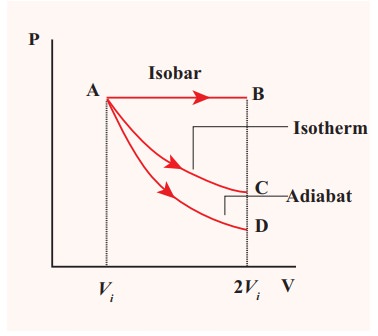
The area under the curve AB = Work done during the isobaric process
The area under the curve AC = Work done during the isothermal process
The area under the curve AD= Work done during the adiabatic process
From the PV diagram the area under the curve AB is more, implying that the work done in isobaric process is highest and work done in adiabatic process is least.
(d) In an adiabatic process no heat enters into the system or leaves from the system. In an isobaric process the work done is more so heat supplied should be more compared to an isothermal process.
EXAMPLE 8.21
500 g of water is heated from 30┬░C to 60┬░C. Ignoring the slight expansion of water, calculate the change in internal energy of the water? (specific heat of water 4184 J/kg.K)
Solution
When the water is heated from 30┬░C to 60┬░C,there is only a slight change in its volume. So we can treat this process as isochoric. In an isochoric process the work done by the system is zero. The given heat supplied is used to increase only the internal energy.
ŌłåU = Q = msv ŌłåT
The mass of water = 500 g =0.5 kg
The change in temperature = 30K
The heat Q = 0.5├Ś4184├Ś30 = 62.76 kJ
Cyclic processes
EXAMPLE 8.22
The PV diagrams for a thermodynamical system is given in the figure below. Calculate the total work done in each of the cyclic processes shown.

Solution
In the case (a) the closed curve is anticlockwise. So the net work done is negative, implying that the work done on the system is greater than the work done by the system. The area under the curve BC will give work done on the gas (isobaric compression) and area under the curve DA (work done by the system) will give the total work done by the system.
Area under the curve BC = Area of rectangle BC12 = 1 ├Ś 4= ŌłÆ 4J
Area under the curve DA = 1 ├Ś 2= + 2J
Net work done in cyclic process = ŌłÆ4 + 2= ŌłÆ2 J
Reversible process
EXAMPLE 8.23
Give some examples of irreversible processes.
All naturally occuring processes are irreversible. Here we give some interesting examples.
(a) When we open a gas bottle, the gas molecules slowly spread into the entire room. These gas molecules can never get back in to the bottle.
(b) Suppose one drop of an ink is dropped in water, the ink droplet slowly spreads in the water. It is impossible to get the ink droplet back.
(c) When an object falls from some height, as soon as it hits the earth it comes to rest. All the kinetic energy of the object is converted to kinetic energy of molecules of the earth surface, molecules of the object and small amount goes as sound energy. The spreaded kinetic energy to the molecules never collected back and object never goes up by itself.
Note that according to first law of thermodynamics all the above processes are possible in both directions. But second law of thermodynamics forbids The processes to occur in the reverse direction. The second law of thermodynamics is one of the very important laws of nature. It controls the way the natural processes occur.
Related Topics