Isothermal process

THERMODYNAMIC PROCESSES

Isothermal process

It is a process in which the temperature remains constant but the pressure and volume of a thermodynamic system will change. The ideal gas equation is

PV = µRT

Here, T is constant for this process

So the equation of state for isothermal process is given by

PV = constant

This implies that if the gas goes from one equilibrium state (P₁,V₁) to another equilibrium state (P₂,V₂) the following relation holds for this process

Since PV = constant, P is inversely proportional toV (P ∝1/V ). This implies that PV graph is a hyperbola. The pressure-volume graph for constant temperature is also called isotherm.

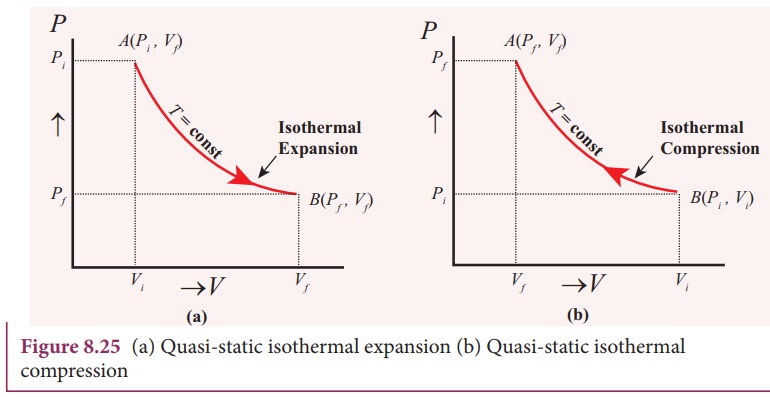
Figure 8.25 shows the PV diagram for quasi-static isothermal expansion and quasi-static isothermal compression.

We know that for an ideal gas the internal energy is a function of temperature only. For an isothermal process since temperature is constant, the internal energy is also constant. This implies that dU or ∆U = 0.

For an isothermal process, the first law of thermodynamics can be written as follows,

From equation (8.30), we infer that the heat supplied to a gas is used to do only external work. It is a common misconception that when there is flow of heat to the system, the temperature will increase. For isothermal process this is not true. The isothermal compression takes place when the piston of the cylinder is pushed. This will increase the internal energy which will flow out of the system through thermal contact. This is shown in Figure 8.26.

Examples:

(i) When water is heated, at the boiling point, even when heat flows to water, the temperature will not increase unless the water completely evaporates. Similarly, at the freezing point, when the ice melts to water, the temperature of ice will not increase even when heat is supplied to ice.

(ii) All biological processes occur at constant body temperature (37°C).

Work done in an isothermal process:

Consider an ideal gas which is allowed to expand quasi-statically at constant temperature from initial state (P_i,V_i) to the final state (P_f, V_f). We can calculate the work done by the gas during this process. From equation (8.17) the work done by the gas,

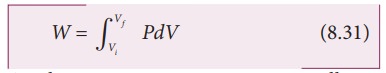
As the process occurs quasi-statically, at every stage the gas is at equilibrium with the surroundings. Since it is in equilibrium at every stage the ideal gas law is valid. Writing pressure in terms of volume and temperature,

Substituting equation (8.32) in (8.31) we get

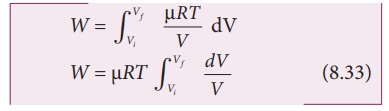
In equation (8.33), we take μRT out of the integral, since it is constant throughout the isothermal process.

By performing the integration in equation (8.33), we get

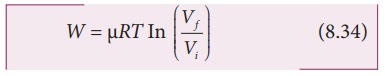
Since we have an isothermal expansion, V_f/V_i >1, so In(V_f/V_i) > 0. As a result the work done by the gas during an isothermal expansion is positive.

The above result in equation (8.34) is true for isothermal compression also. But in an isothermal compression V_f/V_i < 1. so ln(V_f/V_i) <0.

As a result the work done on the gas in an isothermal compression is negative.

In the PV diagram the work done during the isothermal expansion is equal to the area under the graph as shown in Figure 8.27

Similarly for an isothermal compression, the area under the PV graph is equal to the work done on the gas which turns out to be the area with a negative sign.

EXAMPLE 8.16

A 0.5 mole of gas at temperature 300 K expands isothermally from an initial volume of 2 L to 6 L

(a) What is the work done by the gas?

(b) Estimate the heat added to the gas?

(c) What is the final pressure of the gas? (The value of gas constant, R = 8.31 J mol-1 K^-1)

Solution

(a) We know that work done by the gas in an isothermal expansion

Since µ = 0.5

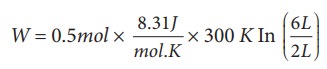
W = 1.369 kJ

Note that W is positive since the work is done by the gas.

(b) From the First law of thermodynamics, in an isothermal process the heat supplied is spent to do work.

Therefore, Q = W = 1.369 kJ. Thus Q is also positive which implies that heat flows in to the system.

(c) For an isothermal process

P_iV_i = P_fV_f = µRT

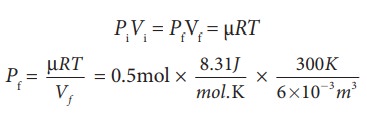
=207.75 k Pa

EXAMPLE 8.17

The following PV curve shows two isothermal processes for two different temperatures and. Identify the higher temperature of these two.

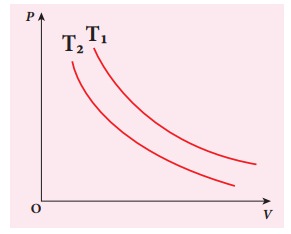
Solution

To determine the curve corresponding to higher temperature, draw a horizontal line parallel to x axis as shown in the figure. This is the constant pressure line. The volumes V₁ and V₂ belong to same pressure as the vertical lines from V₁ and V₂ meet the constant pressure line.

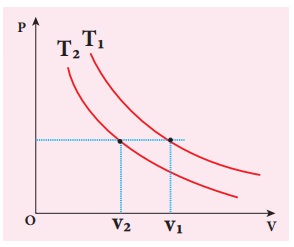
At constant pressure, higher the volume of the gas, higher will be the temperature. From the figure, as V₁ > V₂ we conclude T₁ > T₂. In general the isothermal curve closer to the origin, has lower temperature.