Cyclic processes and PV diagram for a cyclic process

Cyclic processes

This is a thermodynamic process in which the thermodynamic system returns to its initial state after undergoing a series of changes. Since the system comes back to the initial state, the change in the internal energy is zero. In cyclic process, heat can flow in to system and heat flow out of the system. From the first law of thermodynamics, the net heat transferred to the system is equal to work done by the gas.

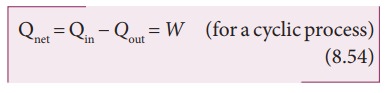
PV diagram for a cyclic process

In the PV diagram the cyclic process is represented by a closed curve.

Let the gas undergo a cyclic process in which it returns to the initial stage after an expansion and compression as shown in Figure 8.39

Let W₁ be the work done by the gas during expansion from volume V₁ to volume V₂. It is equal to area under the graph CBA as shown in Figure 8.40 (a) .

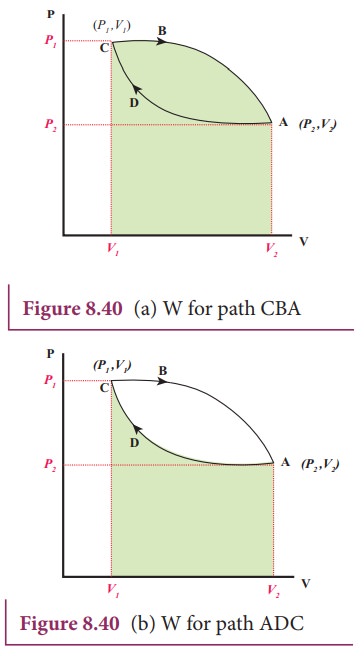
Let W₂ be the work done on the gas during compression from volume V₂ to volume V₁. It is equal to the area under the graph ADC as shown in Figure 8.40 (b)

The total work done in this cyclic process = W₁ - W₂ = Green shaded area inside the loop, as shown in Figure 8.41.

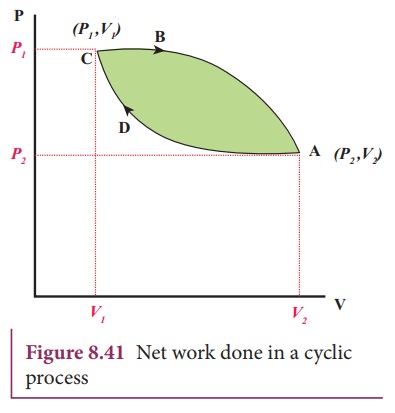
Thus the net work done during the cyclic process shown above is not zero. In general the net work done can be positive or negative. If the net work done is positive, then work done by the system is greater than the work done on the system. If the net work done is negative then the work done by the system is less than the work done on the system.

EXAMPLE 8.22

The PV diagrams for a thermodynamical system is given in the figure below. Calculate the total work done in each of the cyclic processes shown.

Solution

In the case (a) the closed curve is anticlockwise. So the net work done is negative, implying that the work done on the system is greater than the work done by the system. The area under the curve BC will give work done on the gas (isobaric compression) and area under the curve DA (work done by the system) will give the total work done by the system.

Area under the curve BC = Area of rectangle BC12 = 1 × 4= − 4J

Area under the curve DA = 1 × 2= + 2J

Net work done in cyclic process = −4 + 2= −2 J

In the case (b) the closed curve is clockwise. So the net work done is positive, implying that the work done on the system is less than the work done by the system. Area under the curve BC will give work done on the gas (isobaric compression) and area under the curve AB will give the total work done by the system.

Area under the curve AB = rectangle area+ triangle area = (1×2) + 1/₂ × 1×2 = +3J

Area under the curve BC = rectangle area = 1 × 2 = − 2J

Network done in the cyclic process = 1 J, which is positive.

In the case (c) the closed curve is anticlockwise. So the net work done is negative, implying that the work done on the system is greater than work done by the system. The area under the curve AB will give the work done on the gas (isobaric compression) and area under the curve CA (work done by the system) will give the total work done by the system.

The area under the curve AB =Rectangle of area = 4 × 1 = - 4J

The area under the curve CA = Rectangle area + triangle area = (1×2) + 1/2 × 1×2 = +3J The total work in the cyclic process = -1 J. It is negative