Chapter: 11th Physics : UNIT 8 : Heat and Thermodynamics
NewtonŌĆÖs law of cooling
NewtonŌĆÖs
law of cooling
NewtonŌĆÖs law of cooling states that
the rate of loss of heat of a body is directly proportional to the di’¼Ćerence in the temperature between
that body and its surroundings .
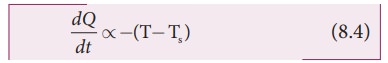
The
negative sign indicates that the quantity of heat lost by liquid goes on
decreasing with time. Where,
T
= Temperature of the object
Ts
= Temperature of the surrounding
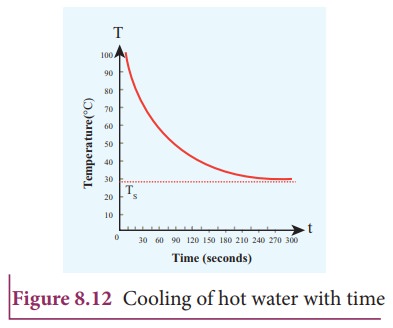
From
the graph in Figure 8.12 it is clear that the rate of cooling is high initially
and decreases with falling temperature.
Let
us consider an object of mass m and specific heat capacity s at temperature T. Let Ts be the
temperature of the surroundings. If the
temperature falls by a small amount dT in time dt, then the amount of heat lost
is,

Where
a is some positive constant.
From
equation (8.6) and (8.7)

Where
b1 is the constant of integration.
taking exponential both sides, we get
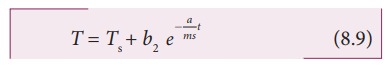
here
b2 = eb1 = constant
EXAMPLE 8.8
A
hot water cools from 92┬░C to 84┬░C in 3 minutes when the room temperature is
27┬░C. How long will it take for it to cool from 65┬░C to 60┬░C?
The
hot water cools 8┬░C in 3 minutes. The average temperature of 92┬░C and 84┬░C is
88┬░C. This average temperature is 61┬░C above room temperature. Using equation
(8.8)
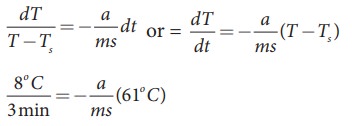
Similarly
the average temperature of 65┬░C and 60┬░C is 62.5┬░C. The average temperature is
35.5┬░C above the room temperature. Then we can write
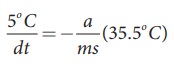
By
diving both the equation, we get
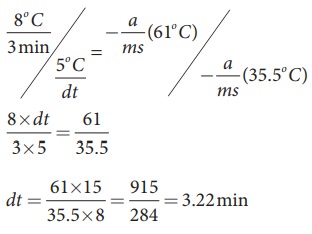
Related Topics