Chapter: 11th Physics : UNIT 8 : Heat and Thermodynamics
Solved Example Problems for Physics : Heat and Thermodynamics
Numerical Problems
1. Calculate the number of moles of air is in the inflated balloon at room temperature as shown in the figure.

The radius of the balloon is 10 cm, and pressure inside the balloon is 180 kPa.
Answer
The radius of the
balloon R = 10 ├Ś 10-2 m
The pressure inside the
balloon P = 1.8 ├Ś 105 P
Room temperature
T = 303 k (273 + 30)
Number of moles of air ╬╝
= ?

V - volume of air in
balloon
V=- 4/3 IR3
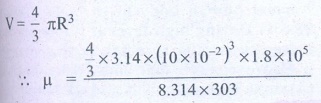
╬╝ = 0.3 moles
Answer: ╬╝ Ōēģ 0.3 mol
2. In the planet Mars, the average temperature is around -53┬░C and atmospheric pressure is 0.9 kPa. Calculate the number of moles of the molecules in unit volume in the planet Mars? Is this greater than that in earth?
Solution
Average temperature of
the mass T = -53┬░C
Atmospheric pressure P
= 0.9 ├Ś 103 P
Volume V = 1 m3
Number of moles n = ?
╬╝mass = VP /
RT = 0.9├Ś103 / 8.314x220 = 0.38 mol
Me = 0.38
mol.
Answer: ╬╝Mars = 0.49 mol
╬╝Earth Ōēģ 40 mol
3. An insulated container of gas has two chambers separated by an insulating partition. One of the chambers has volume V1 and contains ideal gas at pressure P1 and temperature T1. The other chamber has volume V2 and contains ideal gas at pressure P2 and temperature T2. If the partition is removed without doing any work on the gases, calculate the final equilibrium temperature of the container.
Solution:
The volume pressure and
temperature of the gas in first chamber is V1, P1 & T1
By conservation of energy
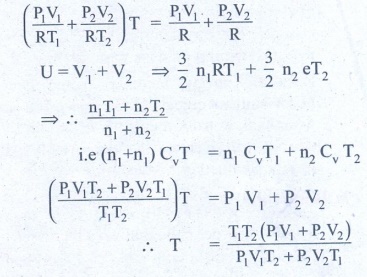

4. The temperature of a uniform rod of length L having a coefficient of linear expansion ╬▒L is changed by ŌłåT. Calculate the new moment of inertia of the uniform rod about axis passing through its center and perpendicular to an axis of the rod.
Solution:
M.I of uniform rod of
mass M. length l about its center
& perpendicular is

When rod is heated by
temperature ΔT, there is increase in length of rod Δl
╬öl = l╬▒L╬öT ŌĆ”ŌĆ”ŌĆ” (1)
(╬▒L -
coefficient of linear expression)
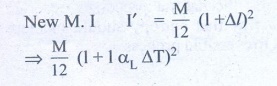
We get substituting Δl from (1)
I' = Ml2 /12 (1+ αL ΔT)2
I' = (1+ αL ΔT)2
(from equation (A)
Answer: I' = I (1 + ╬▒L ŌłåT)2
5. Draw the TP diagram (P-x axis, T-y axis), VT(T-x axis, V-y axis) diagram for
a. Isochoric process
b. Isothermal process
c. isobaric process

6. A man starts bicycling in the morning at a temperature around 25┬░C, he checked the pressure of tire which is equal to be 500 kPa. Afternoon he found that the absolute pressure in the tyre is increased to 520 kPa. By assuming the expansion of tyre is negligible, what is the temperature of tyre at afternoon?

Answer: T= 36.9┬░C
7. Normal human body of the temperature is 98.6┬░F. During high fever if the temperature increases to 104┬░F, what is the change in peak wavelength that emitted by our body? (Assume human body is a black body)

Answer: (a) ╬╗max Ōēł 9348 nm at 98.6┬░F (b) ╬╗max Ōēł 9258 nm at 104┬░F
8. In an adiabatic expansion of the air, the volume is increased by 4%, what is percentage change in pressure? (For air ╬│ = 1.4)

Answer: 5.6%
9. In a petrol engine, (internal combustion engine) air at atmospheric pressure and temperature of 20┬░C is compressed in the cylinder by the piston to 1/8 of its original volume. Calculate the temperature of the compressed air.
(For air ╬│ = 1.4)
At temperature T,
Atmospheric pressure of
air = 1 atm
Initial volume of air V1=
V m3
Initial temperature of
air T1 = 20┬░C
= 20+273 = 293K
At temperature T2
Volume of the air is
compressed by a factor of ŌĆō 1/8
The new volume V2
= V. (1/8) m3
╬│= 1.4
The atmospheric
pressure of the gas at final temperature T2 = ?
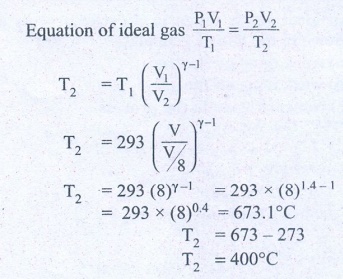
Answer: T Ōēģ 400┬░C
10. Consider the following cyclic process consist of isotherm, isochoric and isobar which is given in the figure.
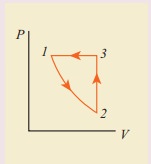
Draw the same cyclic process qualitatively in the V-T diagram where T is taken along x direction and V is taken along y-direction. Analyze the nature of heat exchange in each process.
Solution
In element 1-2, the gas
undergoes isothermal expansions. It receiverŌĆÖs certain amount of heat from the
outside of spends all this heat in doing work the internal energy of the gas
remains unchanged.
In element 2-3, the gas
is heated isochorically (at constant volume). Since its volume does not change,
no work is done. The internal energy of the gas is increased only due to the
heat transferred to the gas from the outside.
In element 3-1, the gas
is compressed isobarically (at constant pressure) of its temperature drops work
is done on the gas, but its internal energy is reduced. This means the gas
intensively gives up heat to the medium.
Answer: T= 36.9┬░C

Process 1 to 2 = increase in volume. So heat must be added.
Process 2 to 3 = Volume remains constant. Increase in temperature. The given heat is used to increase the internal energy.
Process 3 to 1 : Pressure remains constant. Volume and Temperature are reduced. Heat flows out of the system. It is an isobaric compression where the work is done on the system.
11. An ideal gas is taken in a cyclic process as shown in the figure. Calculate
(a) work done by the gas.
(b) work done on the gas
(c) Net work done in the process
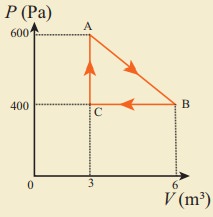

Answer: (a) W = +1.5kJ
(b) W = ŌłÆ1.2kJ
(c) W = +300J.
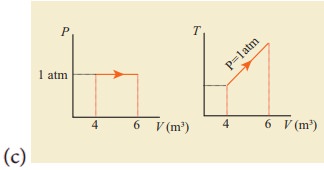
12. For a given ideal gas 6 ├Ś 105J heat energy is supplied and the volume of gas is increased from 4 m3 to 6 m3 at atmospheric pressure. Calculate (a) the work done by the gas (b) change in internal energy of the gas (c) graph this process in PV and TV diagram.
Solution
Heat energy supplied to
the gas Q = 6 ├Ś 105J
Change in Volume ΔV =
(6 - 4) = 2m3
(a) Work done by the
gas W =?
Atmospheric pressure
P = 1.013 ├Ś 105
Nm-2
W = P.ΔV
W = 1.013 ├Ś 105
├Ś 2
= 2.026 ├Ś 105 (or) 202.6 kJ
(b) Change in internal
energy ΔU =?
Δu = W = Q - P. ΔV
= 6 ├Ś 105-2.026
├Ś 105
= 3.974 ├Ś 105J
(or) 397.4kJ
Δu = 397 kJ.
(c)
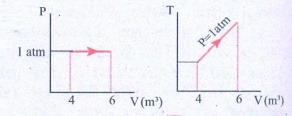
Answer: (a) W = +202.6 kJ
(b) dU = 397.4 kJ
13. Suppose a person wants to increase the efficiency of the reversible heat engine that is operating between 100┬░C and 300┬░C. He had two ways to increase the efficiency. (a) By decreasing the cold reservoir temperature from 100┬░C to 50┬░C and keeping the hot reservoir temperature constant (b) by increasing the temperature of the hot reservoir from 300┬░C to 350┬░C by keeping the cold reservoir temperature constant. Which is the suitable method?
Solution
Temperature of sin x T2 = 100┬░C + 273 = 373K
Temperature of sin x T1 = 300┬░C + 273 = 573 K
Efficiency ╬Ę = ?

Answer: Initial efficiency = 44.5%
Efficiency in method (a) =52 %
Efficiency in method (b) =48 %
Method (a) is more efficient.
14. A Carnot engine whose efficiency is 45% takes heat from a source maintained at a temperature of 327┬░C. To have an engine of efficiency 60% what must be the intake temperature for the same exhaust (sink) temperature?
Solution
Efficiency of Carnot
engine ╬Ę1 = 45%
Efficiency of Carnot
temperature of source T1 = 327┬░C
Efficiency of Carnot
temperature of sink T2 = ?
= 327 + 273 = 600 K
Efficiency of carnot
temperature ╬Ę2 = 60%
when efficiency of
Carnot temperature of source T =?

Answer: 552┬░C
15. An ideal refrigerator keeps its content at 0┬░C while the room temperature is 27┬░C. Calculate its coefficient of performance.
Solution
Content placed at
temperature TL = 0┬░C + 273 = 273K
Room temperature TH
= 27┬░C + 273 = 300 K
Coefficient of
performance ╬▓ = ?
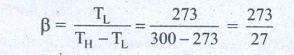
╬▓ = 10.11
Answer: ╬▓=10.11
EXAMPLE 8.1
a. ŌĆśA lake has more rainŌĆÖ.
b. ŌĆśA hot cup of coffee has more heatŌĆÖ. What is wrong in these two statements?
Solution
a. When it rains, lake receives water from the cloud. Once the rain stops, the lake will have more water than before raining. Here ŌĆśrainingŌĆÖ is a process which brings water from the cloud. Rain is not a quantity rather it is water in transit. So the statement ŌĆślake hasmore rainŌĆÖ is wrong, instead the ŌĆślake has more waterŌĆÖ will be appropriate.
b. When heated, a cup of coffee receives heat from the stove. Once the coffee is taken from the stove, the cup of coffee has more internal energy than before. ŌĆśHeatŌĆÖ is the energy in transit and which flows from an object at higher temperature to an object at lower temperature. Heat is not a quantity. So the statement ŌĆśA hot cup of coffee has more heatŌĆÖ is wrong, instead ŌĆścoffee is hotŌĆÖ will be appropriate.
EXAMPLE 8.2
A student comes to school by a bicycle whose tire is filled with air at a pressure 240 kPa at 27┬░C. She travels 8 km to reach the school and the temperature of the bicycle tire increases to 39┬░C. What is the change in pressure in the tire when the student reaches school?

Solution
We can take air molecules in the tire as an ideal gas. The number of molecules and the volume of tire remain constant. So the air molecules at 27┬░C satisfies the ideal gas equation P1V1 = NkT1 and at 39┬░C it satisfies P2V2 = NkT2
But we know
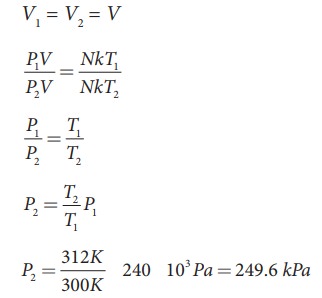
EXAMPLE 8.3
When a person breaths, his lungs can hold up to 5.5 Litre of air at body temperature 37┬░C and atmospheric pressure (1 atm =101 kPa). This Air contains 21% oxygen. Calculate the number of oxygen molecules in the lungs.
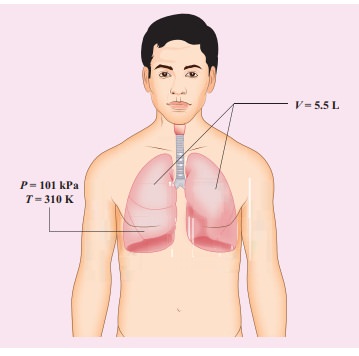
Solution
We can treat the air inside the lungs as an ideal gas. To find the number of molecules, we can use the ideal gas law.
PV = NkT
Here volume is given in the Litre. 1 Litre is volume occupied by a cube of side 10 cm. 1Litre = 10cm ├Ś 10cm ├Ś 10cm = 10-3 m3
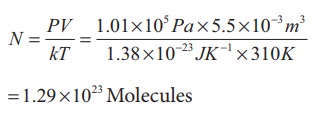
Only 21% of N are oxygen. The total number of oxygen molecules
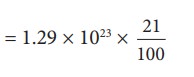
Number of oxygen molecules = 2.7 ├Ś 1022 molecules
EXAMPLE 8.4
Calculate the volume of one mole of any gas at STP and at room temperature (300K) with the same pressure 1 atm.
Solution:
Here STP means standard temperature (T=273K or 0┬░C) and Pressure (P=1 atm or 101.3 kPa)
We can use ideal gas equation V = ╬╝RT / P.
By substituting the values
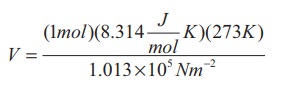
=22.4 ├Ś 10-3 m3
We know that 1 Litre (L) = =10-3m3. So we can conclude that 1 mole of any ideal gas has volume 22.4 L.
By multiplying 22.4L by 300/273KK we get the volume of one mole of gas at room temperature. It is 24.6 L.
EXAMPLE 8.5
Estimate the mass of air in your class room at NTP. Here NTP implies normal temperature (room temperature) and 1 atmospheric pressure.

Solution
The average size of a class is 6m length, 5 m breadth and 4 m height. The volume of the room V = 6 ├Ś 5 ├Ś 4 = 120m3. We can determine the number of mole. At room temperature 300K, the volume of a gas occupied by any gas is equal to 24.6L.
The number of mole ╬╝=
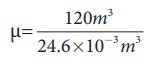
Ōēł4878 mol .
Air is the mixture of about 20% oxygen, 79% nitrogen and remaining one percent are argon, hydrogen, helium, and xenon. The molar mass of air is 29 gmol-1.
So the total mass of air in the room m = 4878 ├Ś 29 = 141.4kg.
Solved Example Problems for Thermal expansion of solids, liquids and gases
EXAMPLE 8.6
Eiffel tower is made up of iron and its height is roughly 300 m. During winter season (January) in France the temperature is 2┬░C and in hot summer its average temperature 25┬░C. Calculate the change in height of Eiffel tower between summer and winter. The linear thermal expansion coefficient for iron ╬▒ = 10 ├Ś10ŌłÆ6 per ┬░C

Solution
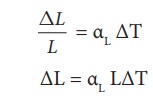
╬öL = 10 ├Ś 10ŌłÆ6 ├Ś 300 ├Ś 23 = 0.69 m=69 cm
Solved Example Problems for Calorimetry
EXAMPLE 8.7
If 5 L of water at 50┬░C is mixed with 4L of water at 30┬░C, what will be the final temperature of water? Take the specific heat capacity of water as 4184 J kg-1K-1.
Solution
We can use the equation

m1 = 5L = 5kg and m2= 4L = 4kg, s1 = s2 and T1=50┬░C =323K and T2 = 30┬░C=303 K.
So
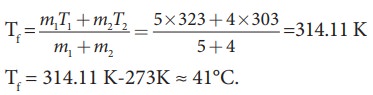
Tf = 314.11 K-273K Ōēł 41┬░C.
Suppose if we mix equal amount of water (m1 = m2) with 50┬░C and 30┬░C, then the final temperature is average of two temperatures.
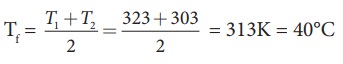
Suppose if both the water are at 30┬░C then the final temperature will also 30┬░C. It implies that they are at equilibrium and no heat exchange takes place between each other.
Solved Example Problems for NewtonŌĆÖs law of cooling
EXAMPLE 8.8
A hot water cools from 92┬░C to 84┬░C in 3 minutes when the room temperature is 27┬░C. How long will it take for it to cool from 65┬░C to 60┬░C?
The hot water cools 8┬░C in 3 minutes. The average temperature of 92┬░C and 84┬░C is 88┬░C. This average temperature is 61┬░C above room temperature. Using equation (8.8)
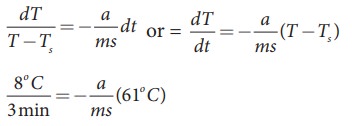
Similarly the average temperature of 65┬░C and 60┬░C is 62.5┬░C. The average temperature is 35.5┬░C above the room temperature. Then we can write
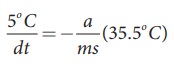
By diving both the equation, we get
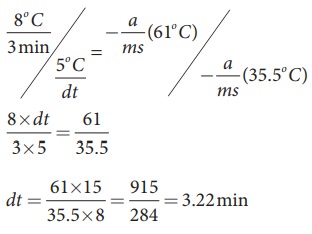
Solved Example Problems for Laws of Heat Transfer
EXAMPLE 8.9
The power radiated by a black body A is EA and the maximum energy radiated was at the wavelength ╬╗A. The power radiated by another black body B is EB = N EA and the radiated energy was at the maximum The power radiated by a black body A is EA and the maximum energy radiated was at the wavelength ╬╗A. The power radiated by another black body B is EB = NEA and the radiated energy was at the maximum wavelength, 1/2 ╬╗A. What is the value of N?
According to2WienŌĆÖs displacement law
╬╗max T = constant for both object A and B

Object B has emitted at lower wavelength compared to A. So the object B would have emitted more energetic radiation than A.
Solved Example Problems for Internal Energy (U)
EXAMPLE 8.10
When you mix a tumbler of hot water with one bucket of normal water, what will be the direction of heat flow? Justify.
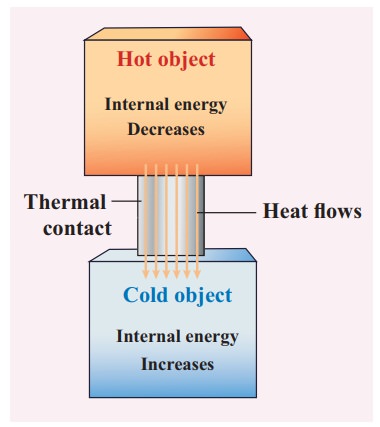
The water in the tumbler is at a higher temperature than the bucket of normal water. But the bucket of normal water has larger internal energy than the hot water in the tumbler. This is because the internal energy is an extensive variable and it depends on the size or mass of the system.
Even though the bucket of normal water has larger internal energy than the tumbler of hot water, heat will flow from water in the tumbler to the water in the bucket. This is because heat flows from a body at higher temperature to the one at lower temperature and is independent of internal energy of the system.
Once the heat is transferred to an object it becomes internal energy of the object. The right way to say is ŌĆśobject has certain amount of internal energyŌĆÖ. Heat is one of the ways to increase the internal energy of a system as shown in the Figure.
EXAMPLE 8.11 (JouleŌĆÖs mechanical equivalent of heat)
A student had a breakfast of 200 food calories. He thinks of burning this energy by drawing water from the well and watering the trees in his school. Depth of the well is about 25 m. The pot can hold 25L of water and each tree requires one pot of water. How many trees can he water? (Neglect the mass of the pot and the energy spent by walking. Take g =10 m s-2)

Solution
To draw 25 L of water from the well, the student has to do work against gravity by burning his energy.
Mass of the water = 25 L = 25 kg (1L=1kg )
The work required to draw 25 kg of water = gravitational potential energy gained by water.
W = mgh = 25├Ś10├Ś25 = 6250 J
The total energy gained from the food = 200 food cal =200 kcal.
= 200├Ś103 ├Ś 4.186 J = 8.37 ├Ś105 J
If we assume that by using this energy the student can drawn ŌĆśnŌĆÖ pots of water from the well, the total energy spent by him = 8.37 ├Ś 105 J = nmgh
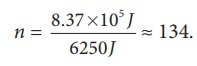
This n is also equal to the number of trees that he can water.
Is it possible to draw 134 pots of water from the well just by having breakfast? No. Actually the human body does not convert entire food energy into work. It is only approximately 20% efficient. It implies that only 20% of 200 food calories is used to draw water from the well. So 20 % of the 134 is only 26 pots of water. It is quite meaningful. So he can water only 26 trees.
The remaining energy is used for blood circulation and other functions of the body. It is to be noted that some energy is always ŌĆśwastedŌĆÖ. Why is it that the body cannot have 100% efficiency? You will find the answer in section 8.9
EXAMPLE 8.12 (First law of thermodynamics)
A person does 30 kJ work on 2 kg of water by stirring using a paddle wheel. While stirring, around 5 kcal of heat is released from water through its container to the surface and surroundings by thermal conduction and radiation. What is the change in internal energy of the system?
Solution
Work done on the system (by the person while stirring), W = -30 kJ = -30,000J
Heat flowing out of the system,
Q = -5 kcal = 5 ├Ś 4184 J =-20920 J
Using First law of thermodynamics
ŌłåU = Q-W
ŌłåU = -20,920 J-(-30,000) J
ŌłåU = -20,920 J+30,000 J = 9080 J
Here, the heat lost is less than the work done on the system, so the change in internal energy is positive.
EXAMPLE 8.13 (First law of thermodynamics)
Jogging every day is good for health. Assume that when you jog a work of 500 kJ is done and 230 kJ of heat is given off. What is the change in internal energy of your body?
Solution

Work done by the system (body),
W = +500 kJ
Heat released from the system (body),
Q = ŌĆō230 kJ
The change in internal energy of a body
= ╬öU= ŌĆō 230 kJ ŌĆō 500 kJ = ŌĆō 730 kJ
EXAMPLE 8.14 (Quasi-static process)
Give an example of a quasi-static process. Consider a container of gas with volume V, pressure P and temperature T. If we add sand particles one by one slowly on the top of the piston, the piston will move inward very slowly. This can be taken as almost a quasi-static process. It is shown in the figure

Sand particles added slowly- quasi-static process
EXAMPLE 8.15 (PV diagram)
A gas expands from volume 1m3 to 2m3 at constant atmospheric pressure.
(a) Calculate the work done by the gas.
(b) Represent the work done in PV diagram.
Solution
(a) The pressure P = 1 atm = 101 kPa, Vf =2 m3 and V1 = 1m3
From equation (8.17) W =
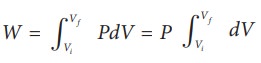
Since P is constant. It is taken out of the integral.
W = P (Vf ŌĆō Vi) = 101├Ś103 ├Ś (2 ŌĆō 1) = 101 kJ
(b) Since the pressure is kept constant, PV diagram is straight line as shown in the figure. The area is equal to work done by the gas.
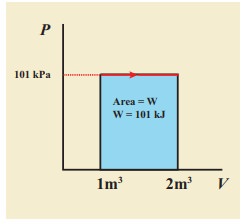
Note the arrow mark in the curve. Suppose the work is done on the system, then volume will decreases and the arrow will point in the opposite direction.
Solved Example Problems for Thermodynamic Processes
Isothermal process
EXAMPLE 8.16
A 0.5 mole of gas at temperature 300 K expands isothermally from an initial volume of 2 L to 6 L
(a) What is the work done by the gas?
(b) Estimate the heat added to the gas?
(c) What is the final pressure of the gas? (The value of gas constant, R = 8.31 J mol-1 K-1)
Solution
(a) We know that work done by the gas in an isothermal expansion
Since ┬Ą = 0.5
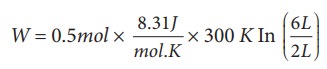
W = 1.369 kJ
Note that W is positive since the work is done by the gas.
(b) From the First law of thermodynamics, in an isothermal process the heat supplied is spent to do work.
Therefore, Q = W = 1.369 kJ. Thus Q is also positive which implies that heat flows in to the system.
(c) For an isothermal process
PiVi = PfVf = ┬ĄRT
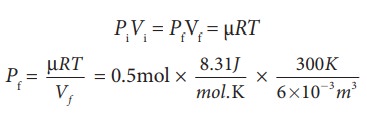
=207.75 k Pa
EXAMPLE 8.17
The following PV curve shows two isothermal processes for two different temperatures and. Identify the higher temperature of these two.
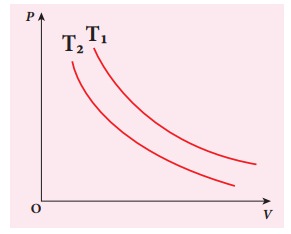
Solution
To determine the curve corresponding to higher temperature, draw a horizontal line parallel to x axis as shown in the figure. This is the constant pressure line. The volumes V1 and V2 belong to same pressure as the vertical lines from V1 and V2 meet the constant pressure line.
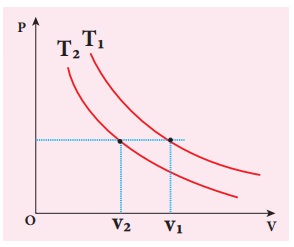
At constant pressure, higher the volume of the gas, higher will be the temperature. From the figure, as V1 > V2 we conclude T1 > T2. In general the isothermal curve closer to the origin, has lower temperature.
Adiabatic process
EXAMPLE 8.18

We often have the experience of pumping air into bicycle tyre using hand pump. Consider the air inside the pump as a thermodynamic system having volume V at atmospheric pressure and room temperature, 27┬░C. Assume that the nozzle of the tyre is blocked and you push the pump to a volume 1/4 of V. Calculate the final temperature of air in the pump? (For air , since the nozzle is blocked air will not flow into tyre and it can be treated as an adiabatic compression).
Solution
Here, the process is adiabatic compression. The volume is given and temperature is to be found. we can use the equation (8.38 )
TiVi╬│-1 = TfVf╬│-1.
Ti = 300 K (273+27┬░C = 300 K)
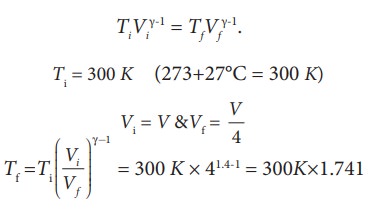
T2 Ōēł 522 K or 2490C
This temperature is higher than the boiling point of water. So it is very dangerous to touch the nozzle of blocked pump when you pump air.
EXAMPLE 8.19
The following graph shows a V-T graph for isobaric processes at two different pressures. Identify which one occurs at higher pressure.
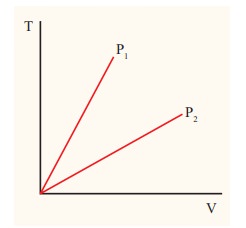
Solution
From the ideal gas equation,
V = (┬ĄR/P)T
V-T graph is a straight line passing the origin.
The slope = ┬ĄR/P
The slope of V-T graph is inversely proportional to the pressure. If the slope is greater, lower is the pressure.
Here P1 has larger slope than P2. So P2 > P1.
Suppose the graph is drawn between T and V (Temperature along the x-axis and Volume along the y-axis) then will we still have P2 > P1?
EXAMPLE 8.20
One mole of an ideal gas initially kept in a cylinder at pressure 1 MPa and temperature 27┬░C is made to expand until its volume is doubled.
(a)ŌĆé How much work is done if the expansion is (i) adiabatic (ii) isobaric (iii) isothermal?
(b) Identify the processes in which change in internal energy is least and is maximum.
(c) Show each process on a PV diagram.
(d) Name the processes in which the heat
(Take ╬│ = 5/3 and R=8.3 J mol-1 K-1)
Solution
(a) (i) In an adiabatic process the work done by the system is
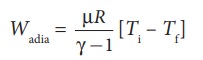
To find the final temperature Tf, we can use adiabatic equation of state.

(ii) In an isobaric process the work done by the system
W = P ŌłåV = P(Vf ŌĆō Vi)
and Vf = 2Vi so W = 2PVi
To find Vi, we can use the ideal gas law for initial state. PiVi = RTi
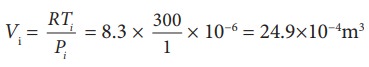
The work done during isobaric process,
W = 2 ├Ś 106 ├Ś 24.9 ├Ś 10ŌłÆ4 = 4.9 kJ
(iii) In an isothermal process the work done by the system,
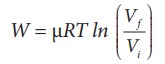
In an isothermal process the initial room temperature is constant.
W = 1 ├Ś 8.3 ├Ś 300 ├Ś ln(2) = 1.7kJ
(b) Comparing all three processes, we see that the work done in the isobaric process is the greatest, and work done in the adiabatic process is the least.
![]()
![]() (c) The PV diagram is shown in the Figure.
(c) The PV diagram is shown in the Figure.
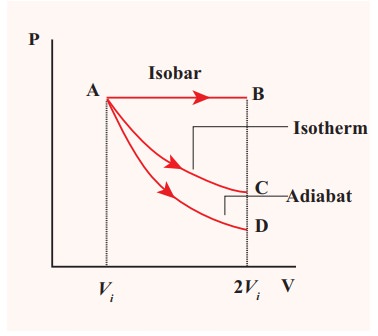
The area under the curve AB = Work done during the isobaric process
The area under the curve AC = Work done during the isothermal process
The area under the curve AD= Work done during the adiabatic process
From the PV diagram the area under the curve AB is more, implying that the work done in isobaric process is highest and work done in adiabatic process is least.
(d) In an adiabatic process no heat enters into the system or leaves from the system. In an isobaric process the work done is more so heat supplied should be more compared to an isothermal process.
EXAMPLE 8.21
500 g of water is heated from 30┬░C to 60┬░C. Ignoring the slight expansion of water, calculate the change in internal energy of the water? (specific heat of water 4184 J/kg.K)
Solution
When the water is heated from 30┬░C to 60┬░C,there is only a slight change in its volume. So we can treat this process as isochoric. In an isochoric process the work done by the system is zero. The given heat supplied is used to increase only the internal energy.
ŌłåU = Q = msv ŌłåT
The mass of water = 500 g =0.5 kg
The change in temperature = 30K
The heat Q = 0.5├Ś4184├Ś30 = 62.76 kJ
Cyclic processes
EXAMPLE 8.22
The PV diagrams for a thermodynamical system is given in the figure below. Calculate the total work done in each of the cyclic processes shown.

Solution
In the case (a) the closed curve is anticlockwise. So the net work done is negative, implying that the work done on the system is greater than the work done by the system. The area under the curve BC will give work done on the gas (isobaric compression) and area under the curve DA (work done by the system) will give the total work done by the system.
Area under the curve BC = Area of rectangle BC12 = 1 ├Ś 4= ŌłÆ 4J
Area under the curve DA = 1 ├Ś 2= + 2J
Net work done in cyclic process = ŌłÆ4 + 2= ŌłÆ2 J
Reversible process
EXAMPLE 8.23
Give some examples of irreversible processes.
All naturally occuring processes are irreversible. Here we give some interesting examples.
(a) When we open a gas bottle, the gas molecules slowly spread into the entire room. These gas molecules can never get back in to the bottle.
(b) Suppose one drop of an ink is dropped in water, the ink droplet slowly spreads in the water. It is impossible to get the ink droplet back.
(c) When an object falls from some height, as soon as it hits the earth it comes to rest. All the kinetic energy of the object is converted to kinetic energy of molecules of the earth surface, molecules of the object and small amount goes as sound energy. The spreaded kinetic energy to the molecules never collected back and object never goes up by itself.
Note that according to first law of thermodynamics all the above processes are possible in both directions. But second law of thermodynamics forbids The processes to occur in the reverse direction. The second law of thermodynamics is one of the very important laws of nature. It controls the way the natural processes occur.
Solved Example Problems for Heat Engine
EXAMPLE 8.24
During a cyclic process, a heat engine absorbs 500 J of heat from a hot reservoir, does work and ejects an amount of heat 300 J into the surroundings (cold reservoir). Calculate the efficiency of the heat engine?
Solution
The efficiency of heat engine is given by
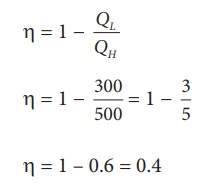
╬╝ = 1 ŌĆō 0.6 = 0.4
The heat engine has 40% efficiency, implying that this heat engine converts only 40% of the input heat into work.
EXAMPLE 8.25
a) A steam engine boiler is maintained at 250┬░C and water is converted into steam. This steam is used to do work and heat is ejected to the surrounding air at temperature 300K. Calculate the maximum efficiency it can have?
Solution
The steam engine is not a Carnot engine, because all the process involved in the steam engine are not perfectly reversible. But we can calculate the maximum possible efficiency of the steam engine by considering it as a Carnot engine.
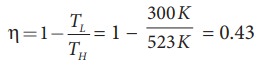
The steam engine can have maximum possible 43% of efficiency, implying this steam engine can convert 43% of input heat into useful work and remaining 57% is ejected as heat. In practice the efficiency is even less than 43%.
EXAMPLE 8.26
There are two Carnot engines A and B operating in two different temperature regions. For Engine A the temperatures of the two reservoirs are 150┬░C and 100┬░C. For engine B the temperatures of the reservoirs are 350┬░C and 300┬░C. Which engine has lesser efficiency?
Solution
The efficiency for engine A = 1 ŌłÆ 373/423 = 0.11. Engine A has 11% efficiency
The efficiency for engine B = 1 - 573/623 = 0.08
Engine B has only 8% efficiency.
Even though the differences between the temperature of hot and cold reservoirs in both engines is same, the efficiency is not same. The efficiency depends on the ratio of the two temperature and not on the difference in the temperature. The engine which operates in lower temperature has highest efficiency.
Solved Example Problems for Refrigerator
EXAMPLE 8.27
A refrigerator has COP of 3. How much work must be supplied to the refrigerator in order to remove 200 J of heat from its interion?
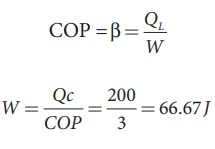
Related Topics