Chapter: 11th Physics : UNIT 8 : Heat and Thermodynamics
MeyerŌĆÖs relation
MeyerŌĆÖs relation
Consider ┬Ą mole of an ideal gas in a container with volume V, pressure P and temperature T.
When the gas is heated at constant volume the temperature increases by dT. As no work is done by the gas, the heat that flows into the system will increase only the internal energy. Let the change in internal energy be dU.
If Cv is the molar specific heat capacity at constant volume, from equation (8.20)

Suppose the gas is heated at constant pressure so that the temperature increases by dT. If ŌĆśQŌĆÖ is the heat supplied in this process and ŌĆśdVŌĆÖ the change in volume of the gas.

If W is the workdone by the gas in this process, then

But from the first law of thermodynamics,

Substituting equations (8.21), (8.22) and (8.23) in (8.24), we get,
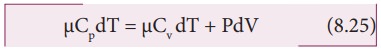
For mole of ideal gas, the equation of state is given by
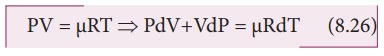
Since the pressure is constant, dP=0
Ōł┤CpdT = CvdT +RdT
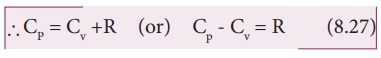
This relation is called MeyerŌĆÖs relation
It implies that the molar specific heat capacity of an ideal gas at constant pressure is greater than molar specific heat capacity at constant volume.
The relation shows that specific heat at constant pressure (sp) is always greater that specific heat at constant volume (sv).
Related Topics