Chapter: 11th Physics : UNIT 8 : Heat and Thermodynamics
Solved Example Problems for Internal Energy (U)
EXAMPLE 8.10
When you mix a tumbler of hot water with one bucket of normal water, what will be the direction of heat flow? Justify.
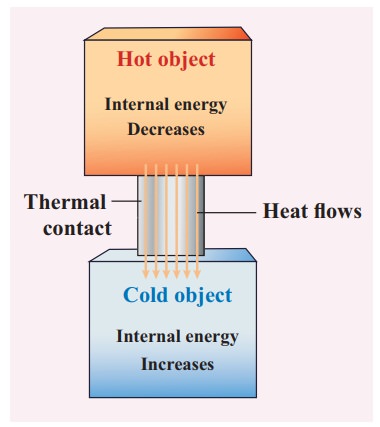
The water in the tumbler is at a higher temperature than the bucket of normal water. But the bucket of normal water has larger internal energy than the hot water in the tumbler. This is because the internal energy is an extensive variable and it depends on the size or mass of the system.
Even though the bucket of normal water has larger internal energy than the tumbler of hot water, heat will flow from water in the tumbler to the water in the bucket. This is because heat flows from a body at higher temperature to the one at lower temperature and is independent of internal energy of the system.
Once the heat is transferred to an object it becomes internal energy of the object. The right way to say is ŌĆśobject has certain amount of internal energyŌĆÖ. Heat is one of the ways to increase the internal energy of a system as shown in the Figure.
EXAMPLE 8.11 (JouleŌĆÖs mechanical equivalent of heat)
A student had a breakfast of 200 food calories. He thinks of burning this energy by drawing water from the well and watering the trees in his school. Depth of the well is about 25 m. The pot can hold 25L of water and each tree requires one pot of water. How many trees can he water? (Neglect the mass of the pot and the energy spent by walking. Take g =10 m s-2)

Solution
To draw 25 L of water from the well, the student has to do work against gravity by burning his energy.
Mass of the water = 25 L = 25 kg (1L=1kg )
The work required to draw 25 kg of water = gravitational potential energy gained by water.
W = mgh = 25├Ś10├Ś25 = 6250 J
The total energy gained from the food = 200 food cal =200 kcal.
= 200├Ś103 ├Ś 4.186 J = 8.37 ├Ś105 J
If we assume that by using this energy the student can drawn ŌĆśnŌĆÖ pots of water from the well, the total energy spent by him = 8.37 ├Ś 105 J = nmgh
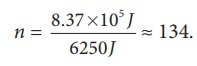
This n is also equal to the number of trees that he can water.
Is it possible to draw 134 pots of water from the well just by having breakfast? No. Actually the human body does not convert entire food energy into work. It is only approximately 20% efficient. It implies that only 20% of 200 food calories is used to draw water from the well. So 20 % of the 134 is only 26 pots of water. It is quite meaningful. So he can water only 26 trees.
The remaining energy is used for blood circulation and other functions of the body. It is to be noted that some energy is always ŌĆśwastedŌĆÖ. Why is it that the body cannot have 100% efficiency? You will find the answer in section 8.9
EXAMPLE 8.12 (First law of thermodynamics)
A person does 30 kJ work on 2 kg of water by stirring using a paddle wheel. While stirring, around 5 kcal of heat is released from water through its container to the surface and surroundings by thermal conduction and radiation. What is the change in internal energy of the system?
Solution
Work done on the system (by the person while stirring), W = -30 kJ = -30,000J
Heat flowing out of the system,
Q = -5 kcal = 5 ├Ś 4184 J =-20920 J
Using First law of thermodynamics
ŌłåU = Q-W
ŌłåU = -20,920 J-(-30,000) J
ŌłåU = -20,920 J+30,000 J = 9080 J
Here, the heat lost is less than the work done on the system, so the change in internal energy is positive.
EXAMPLE 8.13 (First law of thermodynamics)
Jogging every day is good for health. Assume that when you jog a work of 500 kJ is done and 230 kJ of heat is given off. What is the change in internal energy of your body?
Solution

Work done by the system (body),
W = +500 kJ
Heat released from the system (body),
Q = ŌĆō230 kJ
The change in internal energy of a body
= ╬öU= ŌĆō 230 kJ ŌĆō 500 kJ = ŌĆō 730 kJ
EXAMPLE 8.14 (Quasi-static process)
Give an example of a quasi-static process. Consider a container of gas with volume V, pressure P and temperature T. If we add sand particles one by one slowly on the top of the piston, the piston will move inward very slowly. This can be taken as almost a quasi-static process. It is shown in the figure

Sand particles added slowly- quasi-static process
EXAMPLE 8.15 (PV diagram)
A gas expands from volume 1m3 to 2m3 at constant atmospheric pressure.
(a) Calculate the work done by the gas.
(b) Represent the work done in PV diagram.
Solution
(a) The pressure P = 1 atm = 101 kPa, Vf =2 m3 and V1 = 1m3
From equation (8.17) W =
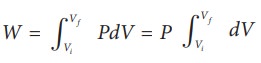
Since P is constant. It is taken out of the integral.
W = P (Vf ŌĆō Vi) = 101├Ś103 ├Ś (2 ŌĆō 1) = 101 kJ
(b) Since the pressure is kept constant, PV diagram is straight line as shown in the figure. The area is equal to work done by the gas.
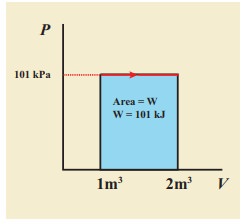
Note the arrow mark in the curve. Suppose the work is done on the system, then volume will decreases and the arrow will point in the opposite direction.
Related Topics