Heat and Thermodynamics | Physics - Book Back Numerical Problems | 11th Physics : UNIT 8 : Heat and Thermodynamics
Chapter: 11th Physics : UNIT 8 : Heat and Thermodynamics
Book Back Numerical Problems
Physics : Heat and Thermodynamics : Book Back Exercise, Example Numerical Question with Answers, Solution : Book Back Numerical Problems
Heat and Thermodynamics | Physics
Numerical Problems
1. Calculate the number of moles of air is in the inflated balloon at room temperature as shown in the figure.

The radius of the balloon is 10 cm, and pressure inside the balloon is 180 kPa.
Answer
The radius of the balloon R = 10 ├Ś 10-2 m
The pressure inside the balloon P = 1.8 ├Ś 105 P
Room temperature
T = 303 k (273 + 30)
Number of moles of air ╬╝ = ?

V - volume of air in balloon
V=- 4/3 IR3
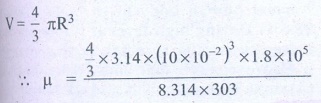
╬╝ = 0.3 moles
Answer: ╬╝ Ōēģ 0.3 mol
2. In the planet Mars, the average temperature is around -53┬░C and atmospheric pressure is 0.9 kPa. Calculate the number of moles of the molecules in unit volume in the planet Mars? Is this greater than that in earth?
Solution
Average temperature of the mass T = -53┬░C
Atmospheric pressure P = 0.9 ├Ś 103 P
Volume V = 1 m3
Number of moles n = ?
╬╝mass = VP / RT = 0.9├Ś103 / 8.314x220 = 0.38 mol
Me = 0.38 mol.
Answer: ╬╝Mars = 0.49 mol
╬╝Earth Ōēģ 40 mol
3. An insulated container of gas has two chambers separated by an insulating partition. One of the chambers has volume V1 and contains ideal gas at pressure P1 and temperature T1. The other chamber has volume V2 and contains ideal gas at pressure P2 and temperature T2. If the partition is removed without doing any work on the gases, calculate the final equilibrium temperature of the container.
Solution:
The volume pressure and temperature of the gas in first chamber is V1, P1 & T1
By conservation of energy
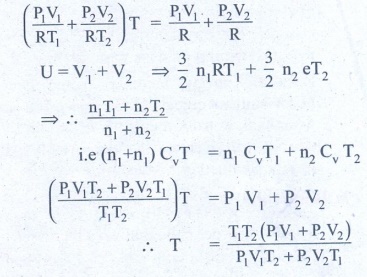
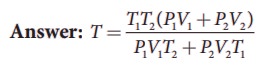
4. The temperature of a uniform rod of length L having a coefficient of linear expansion ╬▒L is changed by ŌłåT. Calculate the new moment of inertia of the uniform rod about axis passing through its center and perpendicular to an axis of the rod.
Solution:
M.I of uniform rod of mass M. length l about its center & perpendicular is

When rod is heated by temperature ΔT, there is increase in length of rod Δl
╬öl = l╬▒L╬öT ŌĆ”ŌĆ”ŌĆ” (1)
(╬▒L - coefficient of linear expression)
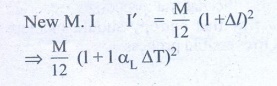
We get substituting Δl from (1)
I' = Ml2 /12 (1+ αL ΔT)2
I' = (1+ αL ΔT)2 (from equation (A)
Answer: I' = I (1 + ╬▒L ŌłåT)2
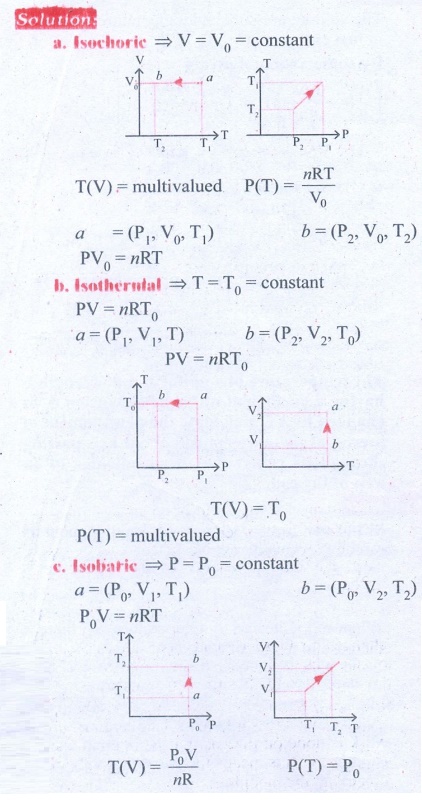
5. Draw the TP diagram (P-x axis, T-y axis), VT(T-x axis, V-y axis) diagram for
a. Isochoric process
b. Isothermal process
c. isobaric process
6. A man starts bicycling in the morning at a temperature around 25┬░C, he checked the pressure of tire which is equal to be 500 kPa. Afternoon he found that the absolute pressure in the tyre is increased to 520 kPa. By assuming the expansion of tyre is negligible, what is the temperature of tyre at afternoon?

Answer: T= 36.9┬░C
7. Normal human body of the temperature is 98.6┬░F. During high fever if the temperature increases to 104┬░F, what is the change in peak wavelength that emitted by our body? (Assume human body is a black body)

Answer: (a) ╬╗max Ōēł 9348 nm at 98.6┬░F (b) ╬╗max Ōēł 9258 nm at 104┬░F
8. In an adiabatic expansion of the air, the volume is increased by 4%, what is percentage change in pressure? (For air ╬│ = 1.4)

Answer: 5.6%
9. In a petrol engine, (internal combustion engine) air at atmospheric pressure and temperature of 20┬░C is compressed in the cylinder by the piston to 1/8 of its original volume. Calculate the temperature of the compressed air.
(For air ╬│ = 1.4)
At temperature T,
Atmospheric pressure of air = 1 atm
Initial volume of air V1= V m3
Initial temperature of air T1 = 20┬░C
= 20+273 = 293K
At temperature T2
Volume of the air is compressed by a factor of ŌĆō 1/8
The new volume V2 = V. (1/8) m3
╬│= 1.4
The atmospheric pressure of the gas at final temperature T2 = ?
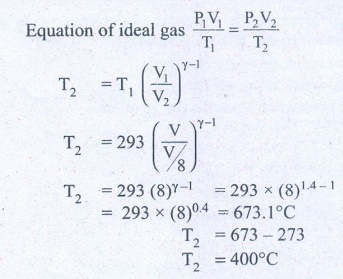
Answer: T Ōēģ 400┬░C
10. Consider the following cyclic process consist of isotherm, isochoric and isobar which is given in the figure.
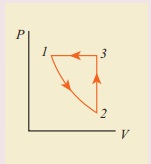
Draw the same cyclic process qualitatively in the V-T diagram where T is taken along x direction and V is taken along y-direction. Analyze the nature of heat exchange in each process.
Solution
In element 1-2, the gas undergoes isothermal expansions. It receiverŌĆÖs certain amount of heat from the outside of spends all this heat in doing work the internal energy of the gas remains unchanged.
In element 2-3, the gas is heated isochorically (at constant volume). Since its volume does not change, no work is done. The internal energy of the gas is increased only due to the heat transferred to the gas from the outside.
In element 3-1, the gas is compressed isobarically (at constant pressure) of its temperature drops work is done on the gas, but its internal energy is reduced. This means the gas intensively gives up heat to the medium.
Answer: T= 36.9┬░C
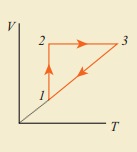
Process 1 to 2 = increase in volume. So heat must be added.
Process 2 to 3 = Volume remains constant. Increase in temperature. The given heat is used to increase the internal energy.
Process 3 to 1 : Pressure remains constant. Volume and Temperature are reduced. Heat flows out of the system. It is an isobaric compression where the work is done on the system.
11. An ideal gas is taken in a cyclic process as shown in the figure. Calculate
(a) work done by the gas.
(b) work done on the gas
(c) Net work done in the process


Answer: (a) W = +1.5kJ
(b) W = ŌłÆ1.2kJ
(c) W = +300J.
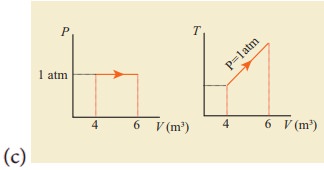
12. For a given ideal gas 6 ├Ś 105J heat energy is supplied and the volume of gas is increased from 4 m3 to 6 m3 at atmospheric pressure. Calculate (a) the work done by the gas (b) change in internal energy of the gas (c) graph this process in PV and TV diagram.
Solution
Heat energy supplied to the gas Q = 6 ├Ś 105J
Change in Volume ΔV = (6 - 4) = 2m3
(a) Work done by the gas W =?
Atmospheric pressure
P = 1.013 ├Ś 105 Nm-2
W = P.ΔV
W = 1.013 ├Ś 105 ├Ś 2
= 2.026 ├Ś 105 (or) 202.6 kJ
(b) Change in internal energy ΔU =?
Δu = W = Q - P. ΔV
= 6 ├Ś 105-2.026 ├Ś 105
= 3.974 ├Ś 105J (or) 397.4kJ
Δu = 397 kJ.
(c)
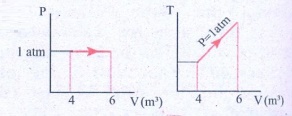
Answer: (a) W = +202.6 kJ
(b) dU = 397.4 kJ
13. Suppose a person wants to increase the efficiency of the reversible heat engine that is operating between 100┬░C and 300┬░C. He had two ways to increase the efficiency. (a) By decreasing the cold reservoir temperature from 100┬░C to 50┬░C and keeping the hot reservoir temperature constant (b) by increasing the temperature of the hot reservoir from 300┬░C to 350┬░C by keeping the cold reservoir temperature constant. Which is the suitable method?
Solution
Temperature of sin x T2 = 100┬░C + 273 = 373K
Temperature of sin x T1 = 300┬░C + 273 = 573 K
Efficiency ╬Ę = ?

Answer: Initial efficiency = 44.5%
Efficiency in method (a) =52 %
Efficiency in method (b) =48 %
Method (a) is more efficient.
14. A Carnot engine whose efficiency is 45% takes heat from a source maintained at a temperature of 327┬░C. To have an engine of efficiency 60% what must be the intake temperature for the same exhaust (sink) temperature?
Solution
Efficiency of Carnot engine ╬Ę1 = 45%
Efficiency of Carnot temperature of source T1 = 327┬░C
Efficiency of Carnot temperature of sink T2 = ?
= 327 + 273 = 600 K
Efficiency of carnot temperature ╬Ę2 = 60%
when efficiency of Carnot temperature of source T =?

Answer: 552┬░C
15. An ideal refrigerator keeps its content at 0┬░C while the room temperature is 27┬░C. Calculate its coefficient of performance.
Solution
Content placed at temperature TL = 0┬░C + 273 = 273K
Room temperature TH = 27┬░C + 273 = 300 K
Coefficient of performance ╬▓ = ?

╬▓ = 10.11
Answer: ╬▓=10.11
Tags : Heat and Thermodynamics | Physics , 11th Physics : UNIT 8 : Heat and Thermodynamics
Study Material, Lecturing Notes, Assignment, Reference, Wiki description explanation, brief detail
11th Physics : UNIT 8 : Heat and Thermodynamics : Book Back Numerical Problems | Heat and Thermodynamics | Physics
Related Topics
11th Physics : UNIT 8 : Heat and Thermodynamics