Heat and Thermodynamics | Physics - Short Questions and Answer | 11th Physics : UNIT 8 : Heat and Thermodynamics
Chapter: 11th Physics : UNIT 8 : Heat and Thermodynamics
Short Questions and Answer
Heat and Thermodynamics | Physics
Short answer questions:
1. ‘An object contains more heat’- is it a right statement? If not why?
●
Heat is not quantity. Heat is energy in transit which flows from higher
temperature object to lower temperature object.
●
Once the heating process is stopped we cannot use the word heat. Heat is the
energy in transit but not energy stored in the body. An object has more heat is
wrong, instead object is hot will be appropriate.
2. Obtain an ideal gas law from Boyle’s and Charles’ law.
●
According to Boyle's law P α 1 /v
●
According to Charle's law V α T. By combining these two equations we have PV =
CT. Here C is positive constant.
●
Constant C is k times the number of particles N.
Here
k is the Boltzmann constant (1.381 × 10-23 JK−1) and it
is found to be universal constant. So the ideal gas law can be stated as
follows PV = NkT.
3. Define one mole.
One
mole of any substance is the amount of that substance which contains Avogadro
number (NA) of particles (such as stoms or molecules).
4. Define specific heat capacity and give its unit.
Specific
heat capacity of a substance is defined as the amount of heat energy required
to raise the temperature of 1kg of substance by 1 Kelvin or 1°C
∆Q
= ms ∆T
Therefore
s = ( 1/m ) ( ∆Q/∆T )
Where
s - specific heat capacity of a substance and its value depends only on the
nature of the substance not on the amount of the substance.
∆Q - Amount of heat energy : ∆T - Change in temperature ; m - Mass of the substance ; The SI unit for specific heat capaity is Jkg−1K−1.
5. Define molar specific heat capacity.
●
Molar specific heat capacity is defined as heat energy required to increase the
temperature of one mole of substance by
1
K or 1°C = 1/μ (∆Q/∆T)
●
Here C is known as molar specific heat capacity of a substance and μ is number
of moles in the substance.
●
The SI unit for molar specific heat capacity is J mol−1 K−1
6. What is a thermal expansion?
●
Termal expansion is the tendency of matter to change in shape, area and volume
due to a change in temperature.
●
All three states of matter (solid, liqid and gas) expand when heated. When a
solid is heated, its atoms vibrate with higher amplitude about their fixed
points. The relative change in the size of solids is small.
7. Give the expressions for linear, area and volume thermal expansions.
Linear
Expansion:
αL=
∆L / Lo∆T; Where αL = coefficient of linear expansion.
∆L
= Change in length; Lo = Original length ; ∆T = Change in
temperature.
Area
Expansion:
αA
= ∆L / Ao∆T ;
Where
αA = coefficient of area expansion.
∆A
= Change in area ;
Ao
= Original area ;
∆T
= Change in temperature
Volume
Expansion:
αV
= ∆A / Vo∆T
Where,
αV = coefficient of volume expansion;
∆V
= Change in volume ;
Vo
= Original volume;
∆T
= Change in temperature.
Unit
of coefficient of linear, area and volumetric expansion of solids is C−1
or K−1.
8. Define latent heat capacity. Give its unit.
●
Latent heat capacity of a substance is defined as the amount of heat energy
required to change the state of a unit mass of the material.
Q = m × L ;
L
= Q / m
●
Where L = latent heat capacity of the substance ; Q = Amount of heat; m = mass
of the substance. The SI unit for Latent heat capacity is J kg−1.
9. State Stefan-Boltzmann law.
●
Stefan Boltzmann law states that, the total amount of heat radiated per second
per unit area of a black body is directly proportional to the fourth power of
its absolute temperature.
●
E ∝ T4 or E = σT4
; Where, σ is known as Stefan's constant. Its value is 5.67 × 10-8 W
m-2 k-4.
10. What is Wien’s law?
●
When's law states that, the wavelength of maximum intensity of emission of a
black body radiation is inversely proportional to the absolute temperature of
the black body.
●
λm ∝ 1/T or λm = b/T.
Where,
b is known as Wien's constant.
●
Its value is 2.898 × 10-3m k.
11. Define thermal conductivity. Give its unit.
●
The quantity of heat transferred through a unit length of a material in a
direction normal to unit surface area due to a unit temperature difference
under steady state conditions is known as thermal conductivity of a material.
●
Q / L = KA∆T / L ; where, K is hnown as the coefficient of thermal
conductivity.
●
The SI unit of thermal conductivity is Js−1m−1K−1 or
Wm−1K−1.
12. What is a black body?
A
black body is an object that absorbs all electromagnetic radiations, it is a
perfect absorber and radiator of energy with no reflecting power.
13. What is a thermodynamic system? Give examples.
Thermodynamic
system: A thermodynamic system is a finite part of the universe. It
is a collection of large number of particles (atoms and molecules) specified by
certain parameters called pressure (P), Volume (V) and Temperature (T). The
remaining part of the universe is called surrounding, Both are separated by a
boundary.
Examples: A
thermodynamic system can be liquid, solid, gas and radiation. Bucket of water,
Air molecules in the room, Human body, Fish in the sea.
14. What are the different types of thermodynamic systems?
Open
system: It can exchange both matter and energy with the environment.
Closed
system: It can exchange energy, but not matter with the environment.
Isolated
system: It can exchange neither energy nor matter with he
environment.
15. What is meant by ‘thermal equilibrium’?
Two
systems are said to be in thermal equilibrium with each other if they are at
the same temperature, which will not change with time.
16. What is mean by state variable? Give example.
In
thermodynamics, the state of a thermodynamic system is represented by a set of
variables called thermodynamic variables.
Examples:
Pressure, temperature, volume and internal energy etc.
The values of these variables completely describe the equilibrium state of a thermodynamic system.
17. What are intensive and extensive variables? Give examples.
Intensive
variable depends on the size or mass of the system.
Example: Volume,
total mass, entropy, internal energy, heat capacity etc.
Intensive
variables do not depend on the size or mass of the system.
Example:
Temperature, pressure, specific heat capacity, density etc.
18. What is an equation of state? Give an example.
Equation
state:
●
The equation which connects the state variables in a specific manner is called
equation of state.
●
A thermodynamic equilibrium is completely specified by these state variables by
the equation of state. If the system is not in thermodynamic equilibrium then
these equations cannot specify the state of the system.
●
Example of equation of state called vander Walls equation. Real gases obey this
equation at thermodynamic equilibrium.
●
The air molecules in the room truly obey vander Walls equation of state. But at
room temperature with low density we can approximate it into an ideal gas.
19. State Zeroth law of thermodynamics.
The
zeroth law of thermodynamics states that if two systems. A and B are in thermal
equilibrium with a third system, C, then A and B are in thermal equilibrium
with each other.
20. Define the internal energy of the system.
●
The internal energy of a thermodynamic system is the sum of kinetic and
potential energies of all the molecules of the systern with respect to the
center of mass of the system.
●
The energy due to molecular motion including translational, rotational and vibrational
motion is called internal kinetic energy (EK). The energy due to
molecular infraction is called internal potential energy (EP).
Example: Bond
energy. U = EK + EP.
21. Are internal energy and heat energy the same? Explain.
●
No, but they are related. If heat energy is added to substance, its internal
energy will increase. Internal energy is the amount of kinetic and potential
energy possessed by particles in a substation.
●
Heat energy concerns only transfer of internal energy from the hotter to a
colder body.
22. Define one calorie.
The
amount of heat required at a pressure of standard atmosphere to rise the
temperature of 1g of water 1°C.
23. Did joule converted mechanical energy to heat energy? Explain.
●
Yes, In his experiment, two masses were attached with a rope and a paddle
wheel. When these masses fall through a distance h due to gravity both the
masses lose potential energy equal to 2mgh.
When
these masses fall, the paddle wheel turns.
●
Due to the turning of wheel inside water, frictional force comes in between the
water and the paddle wheel.
●
This causes a rise in temperature of the water. This implies that gravitational
potential energy is converted to internal energy of water.
●
The temperature of water increases due to the work done by the masses.
24. State the first law of thermodynamics.
Change
in internal energy (∆U) or the system is equal to heat supplied to the system
(Q) minus the work done by the system (W) on the surroundings.
25. Can we measure the temperature of the object by touching it?
●
No. When we stand bare feet with one foot on the carpet and the other on the
tiled floor.
●
Our foot on tiled floor feels cooler than the foot on the carpet even though
both the tiled floor and carpet are at the same room temperature.
●
It is because the tiled floor transfer the heat energy to our skin at higher
rate than the carpet.
●
So the skin is not measuring the actual temperature of the object instead it
measures the rate of heat energy transfer. But if we place a thermometer on the
tiled floor or carpet it will show the same temperature.
26. Give the sign convention for Q and W.
System
gains heat - Q is positive
System
loses heat - Q is negative
Work
done on the system - W is negative
Work
done by the system - W is positive
27. Define the quasi-static process.
●
A quasi-static process is an infinitely slow process in which the system
changes its variables (P.V.T)
●
So slowly such that it remains in thermal, mechanical and chemical euilibrium
with its surroundings throughout.
By
this infinite slow variation, the system is always almost close to equilibrium
state.
28. Give the expression for work done by the gas.
In
general the work done by the gas by increasing the volume from Vi to
Vf is given bty W = vfʃvi pdV
29. What is PV diagram?
PV
diagram is a graph between pressure P and volume V of the system. The P-V
diagram is used to calculate the amount of work done by the gas during
expansion or on the gas during compression.
30. Explain why the specific heat capacity at constant pressure is greater than the specific heat capacity at constant volume.
●
Because when heat is added at constant pressure the substance, expands and
works, i.e. more amount of energy has to be supplied to a constant pressure to increase
the system's temperature by the same amount.
●
Some of this energy is lost due to expansion.
31. Give the equation of state for an isothermal process.
The
equation of state for isothermal process is given by PV = Constant.
32. Give an expression for work done in an isothermal process.
W = μR T In (vf / vi)
33. Express the change in internal energy in terms of molar specific heat capacity.
If
Q is the heat supplied to mole of a gas at constant volume and if the
temperature changes by an amount ∆T, we have Q = μCV ∆T …….. (1)
By
applying the first law of thermodynamics for this constant volume process (W =
O, since dV = O), we have Q = ∆U – O …….. (2)
By
comparing the equations (1) and (2),
∆U
= μ CV ∆T or CV = 1/μ (dU/dT)
If
the limit ∆T goes to zero, we can write
CV
= = 1/μ × dU/dT
Since
the temperature and internal energy are state variable, the above relation
holds true for any process.
34. Apply first law for (a) an isothermal (b) adiabatic (c) isobaric processes.
Isothermal: Q = W; Q
- Heat; W - Work
Adiabatic: ∆U = W
Isobaric; ∆U = Q - P∆U
∆U
- change in internal energy.
35. Give the equation of state for an adiabatic process.
The
equation of state for an adiabatic process is given by PVγ =
Constant. Here γ is called adiabatic exponent (γ = Cp / Cv )
which
depends on the nature of the gas. The equation implies that if the gas goes
from an equilibrium state (PiVi) to another equilibrium
state (Pf, Vf) adiabatically then it satisfies the
relation.
36. Give an equation state for an isochoric process.
The
equation of state for an isochoric process is given by P = (μR/v)T,
Where, μR / v = Constant
37. If the piston of a container is pushed fast inward. Will the ideal gas equation be valid in the intermediate stage? If not, why?
Decrease in volume leading to increase in temperature, work is done on the gas. Ideal gas equation PV = RT. When piston be pushed further the parameters V and R are taken as constant. The equation becomes P = kT. i.e. P ∝ T.
38. Draw the PV diagram for
a. Isothermal process
b. Adiabatic process
c. isobaric process
d. Isochoric process
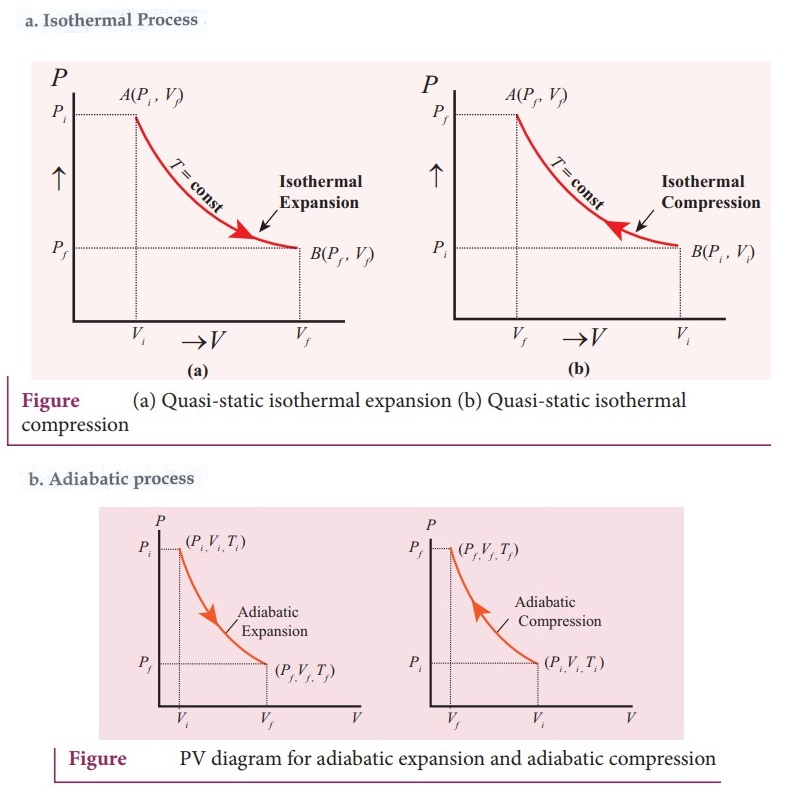
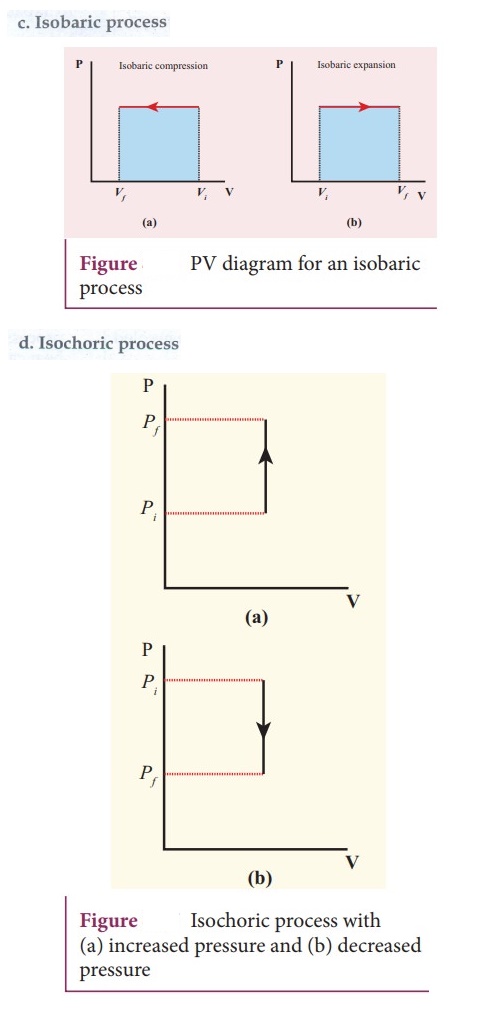
39. What is a cyclic process?
This
is a thermodynamic process in which the thermodynamic system returns to its
initial state after undergoing a series of changes. Since the system comes back
to the initial state, the change in the internal energy is zero. In cyclic
process, heat can flow in to system and heat flow out of the system.
40. What is meant by a reversible and irreversible processes?
Reversible
process:
●
A thermodynamic process can be considered reversible only if it possible to
retrace the path in the opposite direction in such a way that the system and
surroundings pass through the same states as in the initial, direct process.
Example: A
quasi-static isothermal expansion of gas, slow compression and expansion of a
spring.
Irreversible
process: All natural process are irreversible.
●
Irreversible process cannot be plotted in a PV diagram, because these processes
cannot have unique values of pressure, temperature at every stage of the
process.
41. State Clausius form of the second law of thermodynamics
"Heat
always flows from hotter object to colder object
spontaneously". This is known as the Clausius form of second law of
thermodynamics.
42. State Kelvin-Planck statement of second law of thermodynamics.
Kelvin-Planck
statement: It is impossible to construct a heat engine that operates in
a cycle, whose sole effect is to convert the heat completely into work. This
implies that no heat engine in the universe can have 100% efficiency.
43. Define heat engine.
Heat
engine is a device which takes heat as input and converts this heat in to work
by undergoing a cyclic process.
44. What are processes involves in a Carnot engine?
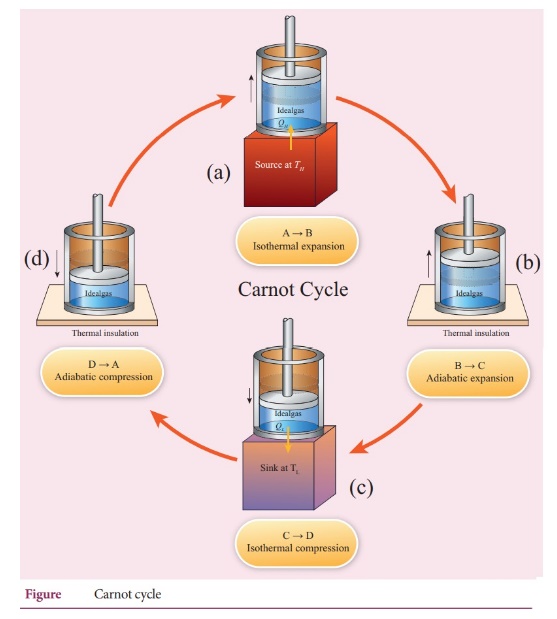
There
are four servisible process in involed in carnot's engine. There are
Step
A to B: Quasi-static isothermal expansion .
Step
B to C: Quasi-static adiabatic expansion.
Step
C to D: Quasi-static Isothermal compression
Step
D to A: Quasi-static compression adiabatic compression.
45. Can the given heat energy be completely converted to work in a cyclic process? If not, when can the heat can completely converted to work?
●
No. In a cyclic process, the complete heat energy is not completely converted
to work.
●
The whole heat cannot be converted into work, as it will violate second law of
thermodynamics.
●
In an Isothermal process the whole heat can be converted into work. For an
isothermal process dQ = dT, which shows that whole heat can be converted into
work.
46. State the second law of thermodynamics in terms of entropy.
●
"For all the processes that occur in nature (irreversible process), the
entropy always increases. For reversible process entropy will not change".
●
Entropy determines the direction in which natural process should occur.
47. Why does heat flow from a hot object to a cold object?
Because
entropy increases when heat flows from hot object to cold object.
48. Define the coefficient of performance.
COP
is a measure of the efficiency of a refrigerator, it is defined as the ration
of heat extracted from the cold body (sink) to the external work done by the
compressor
W.
COP = β [ QL / W]
Related Topics