Thermodynamics - Isobaric process | 11th Physics : UNIT 8 : Heat and Thermodynamics
Chapter: 11th Physics : UNIT 8 : Heat and Thermodynamics
Isobaric process
Isobaric
process
This
is a thermodynamic process that occurs at constant pressure. Even though
pressure is constant in this process, temperature, volume and internal energy
are not constant. From the ideal gas equation, we have

In
an isobaric process the temperature is directly proportional to volume.
V ŌłØ
T (Isobaric
process) (8.44)

This
implies that for a isobaric process, the V-T graph is a straight line passing
through the origin.
If
a gas goes from a state (Vi
,Ti) to ( Vf ,Tf) at constant pressure, then the system satisfies the
following equation

Examples
for Isobaric process:
(i)
When the gas is heated and pushes the piston so that it exerts a force
equivalent to atmospheric pressure plus the force due to gravity then this
process is isobaric. This is shown in Figure 8.33
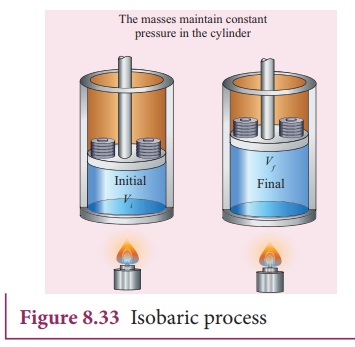
(ii)
Most of the cooking processes in our kitchen are isobaric processes. When the
food is cooked in an open vessel, the pressure above the food is always at
atmospheric pressure. This is shown in Figure 8.34

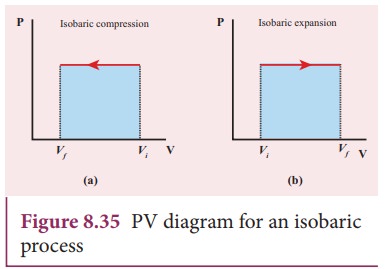
The
PV diagram for an isobaric process is a horizontal line parallel to volume axis
as shown in Figure 8.35.
Figure
8.35 (a) represents isobaric process where volume decreases
Figure
8.35 (b) represents isobaric process where volume increases
The
work done in an isobaric process:
Work
done by the gas

In
an isobaric process, the pressure is constant, so P comes out of the integral,

Where
ŌłåV denotes change in the volume. If ŌłåV is negative, W is also negative. This
implies that the work is done on the gas. If ŌłåV is positive, W is also positive, implying that work is done by
the gas.
The
equation (8.48) can also be rewritten using the ideal gas equation.
From
ideal gas equation
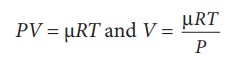
Substituting
this in equation (8.48) we get
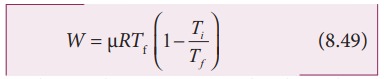
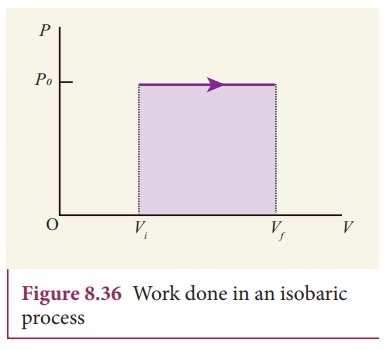
In
the PV diagram, area under the isobaric curve is equal to the work done in
isobaric process. The shaded area in the following Figure8.36 is equal to the
work done by the gas.
The
first law of thermodynamics for isobaric process is given by
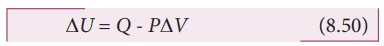
ŌłåU = Q ŌĆō PDV
EXAMPLE 8.19
The
following graph shows a V-T graph for isobaric processes at two different
pressures. Identify which one occurs at higher pressure.
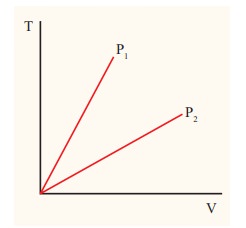
Solution
From the
ideal gas equation,
V = (┬ĄR/P)T
V-T
graph is a straight line passing the origin.
The
slope = ┬ĄR/P
The
slope of V-T graph is inversely proportional to the pressure. If the slope is
greater, lower is the pressure.
Here
P1 has larger slope than P2. So P2 > P1.
Suppose
the graph is drawn between T and V (Temperature along the x-axis and Volume
along the y-axis) then will we still have P2
> P1?
EXAMPLE 8.20
One
mole of an ideal gas initially kept in a cylinder at pressure 1 MPa and
temperature 27┬░C is made to expand until its volume is doubled.
(a)ŌĆé How much work is done if the expansion is (i) adiabatic (ii)
isobaric (iii) isothermal?
(b)
Identify the processes in which change in internal energy is least and is
maximum.
(c)
Show each process on a PV diagram.
(d)
Name the processes in which the heat
(Take
╬│ = 5/3 and R=8.3 J mol-1 K-1)
Solution
(a) (i) In an adiabatic process the work done by the system is
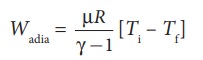
To
find the final temperature Tf, we can use adiabatic equation of
state.

(ii) In an isobaric process the
work done by the system
W = P ŌłåV = P(Vf ŌĆō
Vi)
and
Vf = 2Vi so W = 2PVi
To
find Vi, we can use the
ideal gas law for initial state. PiVi = RTi
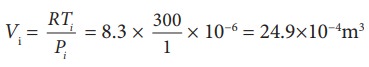
The
work done during isobaric process,
W = 2 ├Ś 106 ├Ś 24.9 ├Ś
10ŌłÆ4 = 4.9 kJ
(iii)
In an isothermal process the work done by the system,
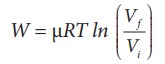
In
an isothermal process the initial room temperature is constant.
W = 1 ├Ś 8.3 ├Ś 300 ├Ś ln(2)
= 1.7kJ
(b) Comparing all three
processes, we
see that the work done
in the isobaric process is the greatest, and work done in the adiabatic process
is the least.
![]()
![]() (c) The PV diagram is shown
in the Figure.
(c) The PV diagram is shown
in the Figure.
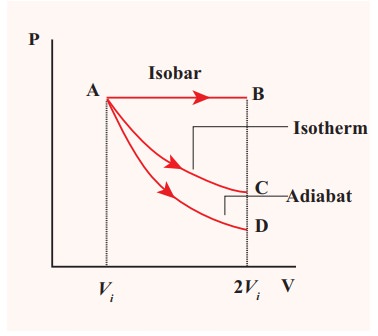
The
area under the curve AB = Work done during the isobaric process
The
area under the curve AC = Work done during the isothermal process
The
area under the curve AD= Work done during the adiabatic process
From
the PV diagram the area under the curve AB is more, implying that the work done
in isobaric process is highest and work done in adiabatic process is least.
(d) In an adiabatic process no heat enters into the system or
leaves from the system. In an isobaric process the work done is more so heat
supplied should be more compared to an isothermal process.
Related Topics