Adiabatic process

Adiabatic process

This is a process in which no heat flows into or out of the system (Q=0). But the gas can expand by spending its internal energy or gas can be compressed through some external work. So the pressure, volume and temperature of the system may change in an adiabatic process.

For an adiabatic process, the first law becomes ∆U = W.

This implies that the work is done by the gas at the expense of internal energy or work is done on the system which increases its internal energy.

The adiabatic process can be achieved by the following methods

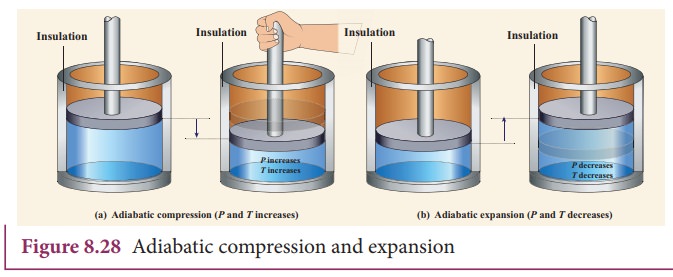
(i) Thermally insulating the system from surroundings so that no heat flows into or out of the system; for example, when thermally insulated cylinder of gas is compressed (adiabatic compression) or expanded (adiabatic expansion) as shown in the Figure 8.28

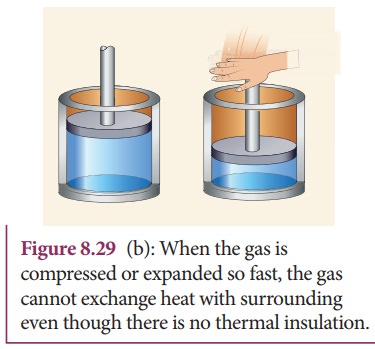
(ii) If the process occurs so quickly that there is no time to exchange heat with surroundings even though there is no thermal insulation. A few examples are shown in Figure 8.29.

Examples:

The equation of state for an adiabatic process is given by

Here γ is called adiabatic exponent (γ = C_p/C_v) which depends on the nature of the gas.

The equation (8.35) implies that if the gas goes from an equilibrium state (P_i,V_i) to another equilibrium state (P_f ,V_f) adiabatically then it satisfies the relation

The PV diagram of an adiabatic expansion and adiabatic compression process are shown in Figure 8.30. The PV diagram for an adiabatic process is also called adiabat Note that the PV diagram for isothermal (Figure 8.25) and adiabatic (Figure 8.30) processes look similar. But actually the adiabatic curve is steeper than isothermal curve.

We can also rewrite the equation (8.35) in terms of T and V. From ideal gas equation, the pressure P = μRT/V. Substituting this equation in the equation (8.35), we have

Note here that is another constant. So it can be written as

The equation (8.37) implies that if the gas goes from an initial equilibrium state (T_i, V_i) to final equilibrium state (T_f, V_f) adiabatically then it satisfies the relation

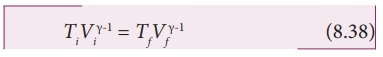
The equation of state for adiabatic process can also be written in terms of T and P as

(The proof of equation (8.39) left as an exercise).

EXAMPLE 8.18

We often have the experience of pumping air into bicycle tyre using hand pump. Consider the air inside the pump as a thermodynamic system having volume V at atmospheric pressure and room temperature, 27°C. Assume that the nozzle of the tyre is blocked and you push the pump to a volume 1/4 of V. Calculate the final temperature of air in the pump? (For air , since the nozzle is blocked air will not flow into tyre and it can be treated as an adiabatic compression).

Solution

Here, the process is adiabatic compression. The volume is given and temperature is to be found. we can use the equation (8.38 )

T_iV_i^γ-1 = T_fV_f^γ-1.

T_i = 300 K   (273+27°C = 300 K)

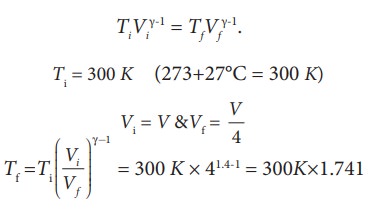
T2 ≈ 522 K or 2490C

This temperature is higher than the boiling point of water. So it is very dangerous to touch the nozzle of blocked pump when you pump air.

Work done in an adiabatic process:

Consider μ moles of an ideal gas enclosed in a cylinder having perfectly non conducting walls and base. A frictionless and insulating piston of cross sectional area A is fitted in the cylinder as shown in Figure 8.31.

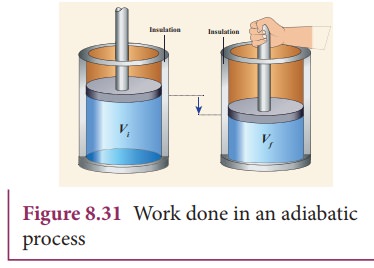
Let W be the work done when the system goes from the initial state (P_i,V_i,T_i) to the final state (P_f,V_f,T_f) adiabatically.

By assuming that the adiabatic process occurs quasi-statically, at every stage the ideal gas law is valid. Under this condition, the adiabatic equation of state is PV^γ=constant (or)

P =  constant/V^γ can be substituted in the equation (8.40), we get

From ideal gas law,

P_fV_f = μRT_f and P_iV_i = μRT_i

Substituting in equation (8.41), we get

In adiabatic expansion, work is done by the gas. i.e., W_adia is positive. As T_i>T_f , the gas cools during adiabatic expansion.

In adiabatic compression, work is done on  the gas. i.e., W_adia is negative. As T_i<T_f, the temperature of the gas increases during adiabatic compression.

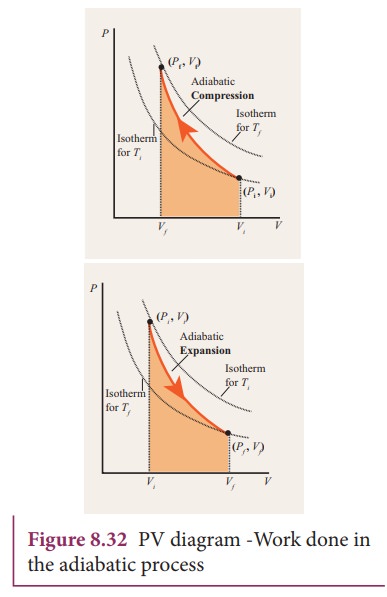
To differentiate between isothermal and adiabatic curves in (Figure 8.32) the adiabatic curve is drawn along with isothermal curve for T_f and T_i. Note that adiabatic curve is steeper than isothermal curve. This is because γ > 1 always.