Heat and Thermodynamics | Physics - Long Questions and Answer | 11th Physics : UNIT 8 : Heat and Thermodynamics
Chapter: 11th Physics : UNIT 8 : Heat and Thermodynamics
Long Questions and Answer
Heat and Thermodynamics | Physics
Long answer Questions:
1. Explain the meaning of heat and work with suitable examples.
Meaning
of heat and work:
ŌŚÅ
When we rub our hand against each other the temperature of the hands increases.
We have done some work on our hands by rubbing. The temperature of the hands
increases due to this work.
ŌŚÅ
If we place our hands on the chin, the temperature of the chin increases.
ŌŚÅ
This is because the hands are at higher temperature than the chin.
ŌŚÅ
In the above example, the temperature of hands is increased due to work and
temperature of the chin is increased due to heat transfer from the hands to the
chin.
ŌŚÅ
By doing work on the system, the temperature in the system will increase and
sometimes may not.
ŌŚÅ
Like heat, work is also not a quantity and through the work, energy is
transferred to the system.
ŌŚÅ
So we cannot use the word ŌĆśthe object contains more work' or ŌĆśless work'.
ŌŚÅ
Either the system can transfer energy to the surrounding by doing work on
surrounding or the surrounding may transfer energy to the system by doing work
on the system.
ŌŚÅ
For the transfer of energy from one body to another body through the process of
work, they need not be at different temperatures.
2. Discuss the ideal gas laws.
Boyle's
law, Charles' law and ideal gas law:
ŌŚÅ
For a given gas at low pressure (density) kept in a container of volume V,
experiments revealed the following information.
ŌŚÅ
When the gas is kept at constant temperature, the pressure of the gas is
inversely proportional to the volume.
P
ŌłØ 1/v known as Boyle's law.
ŌŚÅ
When the gas is kept at constant pressure, the volume of the gas is directly
proportional to absolute temperature. V ŌłØ T. Known
as Charles's law.
ŌŚÅ
By combining these two equation we have PV = CT. Here C is a positive constant.
C
is proportional to the number of particles in the gas container.
ŌŚÅ
If we take two container of same type of gas with same volume V, same pressure
P and same temperature T, then the gas in each container obeys the above
equation. PV = CT.
ŌŚÅ
If the two containers of gas is considered as a single system, then the
pressure and temperature of this combined system will be same but volume will
be twice and number of particles will also be double.
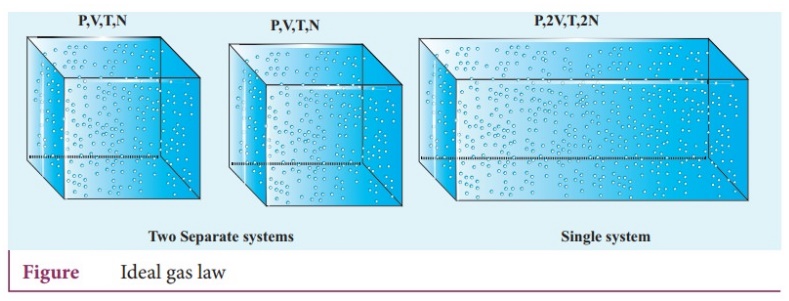
ŌŚÅ
For this combined system, V becomes 2V, so C should also double to match with
the ideal gas equation P(2V)/T = 2C.
ŌŚÅ
It implies that C must depend on the number of particles in the gas and also should
have the dimension of [PV /T]= JKŌłÆ1.
ŌŚÅ We can write the constant C as k times the number of particles N. Here k is the Boltzmann constrit (1.381 ├Ś 10ŌłÆ23 JKŌłÆ1) and it is found to be a universal constant. So the ideal gas law can be stated as follows PV = NkT.
3. Explain in detail the thermal expansion.
ŌŚÅ
Thermal expansion is the tendency of matter to change in shape, area and volume
due to a change in temperature.
ŌŚÅ
All three states of matter (solid, liquid and gas) expand when heated. When a
solid is heated, its atoms vibrate with higher amplitude about their fixed
points. The relative change in the size of solids is small.
ŌŚÅ
Railway tracks are given small gaps so that in the summer, the tracks expand
and do not buckle.
ŌŚÅ
Railroad tracks and bridges have expansion joints to allow them to expand and
contract freely with temperature changes.
ŌŚÅ
Liquids, have less intermolecular forces than solids and hence they expand more
than solids. This is the principle behind the mercury thermometers.
ŌŚÅ
In the case of gas molecules, the intermolecular forces are almost negligible
and hence they expand much more than solids. For example in hot air ballons
when gas particles get heated, they expand and take up more space.
ŌŚÅ
The increase in dimension of a body due to the increase in its temperature is
called thermal expansion
ŌŚÅ
The expansion in length is called liner expansion. Similarly the expansion in
area is termed as area expansion and the expansion in volume is termed as
volume expansion.
Linear Expansion:
In
solids, for a small change in temperature ŌłåT, the fractional change in length [ŌłåL/Lo]
is directly proportional to ŌłåT. (ŌłåL/ Lo) = ╬▒L ŌłåT
Therefore,
╬▒L = ŌłåL / LoŌłåT ; Where, ╬▒L =
coefficient of linear expansion .
ŌłåL
= Change in length ; Lo = Original length ; ŌłåT = Change in temperature,
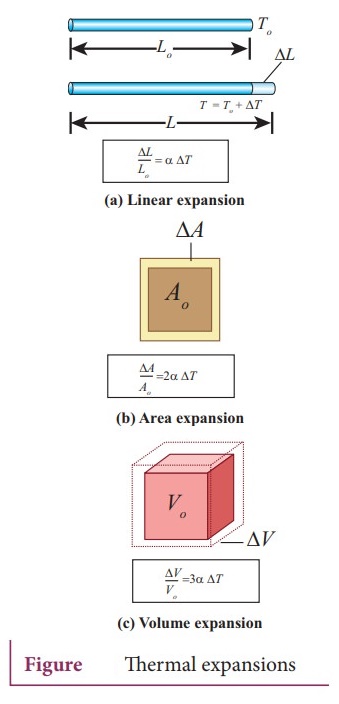
Area
Expansion:
For a small change in temperature ŌłåT the fractional change in area [ŌłåA / Ao] of a substance is directly proportional to ŌłåT and it can be written as ŌłåA/ Ao = ╬▒AŌłåT
Therefore,
╬▒A [ŌłåA / AoŌłåT];
Where
╬▒A = coefficient of area expansion;
ŌłåA
= Change in area;
Ao
= Original area;
ŌłåT
= Change in temperature
Volume Expansion:
For
a small change in temperature ŌłåT the fractional change in volume
[ŌłåA
/ Vo] of a substance is directly proportional to ŌłåT.
ŌłåV
/ Vo = ╬▒V ŌłåT, Therefore, ╬▒V [ŌłåV/VoŌłåT].
Where,
╬▒V = coefficient of volume expansion ; ŌłåV = Change in volume ;
Vo = Original volume ; ŌłåT = Change in temperature. Unit of coefficient of linear, area and volumetric expansion of solids is ┬░CŌłÆ1 or KŌłÆ1.
4. Describe the anomalous expansion of water. How is it helpful in our lives?
Anomalous
expansion of water:
ŌŚÅ
Liquids expand on heating and contract on cooling at moderate temperatures.
ŌŚÅ
But water exhibits an anomalous behavior.
ŌŚÅ
It contracts on heating between 0┬░C and 4┬░C.
ŌŚÅ
The volume of the given amount of water decreases as it is cooled from room
temperature, until it reach 4┬░C.
ŌŚÅ
Below 4┬░C the volume increases and so the density decreases.
ŌŚÅ
The water has a maximum density at 4┬░C.
ŌŚÅ
This behavior of water is called anomalous expansion of water.

ŌŚÅ
In cold contries during the winter season, the surface of the lakes will be at
lower temperature than the bottom.
ŌŚÅ
Since the solid water (ice) has lower density than its liquid form, below 4┬░C,
the frozen water will be on the top surface above the liquid water (ice floats)
ŌŚÅ
This is due to the anomalous expansion of water.
ŌŚÅ
As the water in takes and ponds freeze only at the top the species living in
the lakes will be safe at the bottom.
5. Explain Calorimetry and derive an expression for final temperature when two thermodynamic systems are mixed.
Calorimetry:
ŌŚÅ
Calorimetry means the measurement of the amount of heat released or absorbed by
thermodynamic system during the heating process.
ŌŚÅ
When a body at higher temperature is brought in contact with another body at
lower temperature, the heat lost by the hot body is equal to the heat gained by
the cold body.
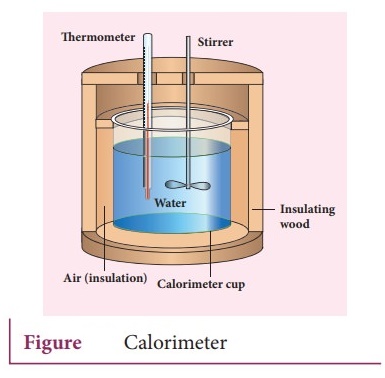
ŌŚÅ
No heat is allowed to escape to the surroundings.
ŌŚÅ
It can be mathematically expressed as Qgain = ŌłÆ Qlost ; Qgain
+ Qlost = 0
ŌŚÅ
Heat gained or lost is measured with a calorimeter.
Usually
the calorimeter is an insulated container of water.
ŌŚÅ
A sample is heated at high temperature (T1) and immersed into water
at room temperature (T2) in the calorimeter. After some time both
sample and water reach a final equilibrium temperature Tf. Since the
calorimeter is insulated, heat given by the hot sample is equal to heat gained
by the water.
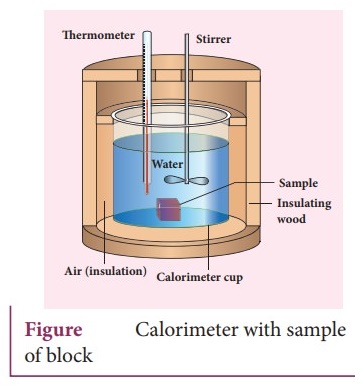
Qgain = ŌłÆ Qlost
ŌŚÅ
The heat lost is denoted by negative sign and heat gained is denoted as
positive.
ŌŚÅ
From the definition of specific heat capacity
Qgain
= m2s2(Tf ŌłÆT2)
Qlost
= m1s1 (Tf ŌĆō T1)
ŌŚÅ
Here s1 and s2 specific heat capacity of hot sample and water respectively.
m2s2(Tf
ŌłÆT2) = m1s1 (Tf ŌĆō T1)
m2s2Tf
ŌłÆ m2s2T2 = - m1s1Tf
+ m1s1T1
m2s2Tf
+ m1s1Tf = m2s2T2
+ m1s1T1
The
final temperature Tf = [ m1s1T1 + m2s2T2
] / [ m1s1 + m2s2 ]
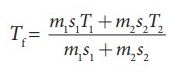
6. Discuss various modes of heat transfer.
Conduction:
Conduction is the process of direct transfer of heat through matter due to
temperature difference. When two objects are in direct contact with one
another, heat will be transferred from the hotter object to the colder one.
Thermal conductivity depends on the nature of the material.
Convection:
Convection is the process in which heat transfer is by actual movement of
molecules in fluids such as liquids and gases. In convection, molecules move
freely from one place to another.
Radiation:
Radiation is a form of energy transfer from one body to another by
electromagnetic waves. Radiation which requires no medium to transfer energy
from one object to another.
Example: 1 Solar energy from the sun, 2. Radiation from room heater.
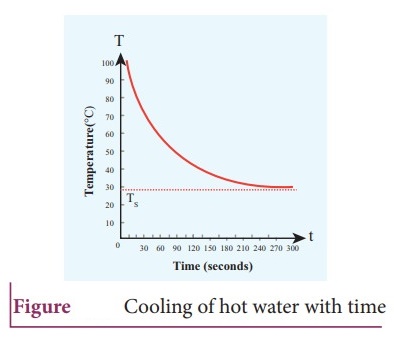
7. Explain in detail NewtonŌĆÖs law of cooling.
Newton's
law of cooling:
ŌŚÅ
Newton's law of cooling states that the rate of loss of heat of a body is
directly proportional to the difference in the temperature between that body
and its surroundings.
dQ/dt
ŌłØ ŌłÆ (TŌłÆTS) ------------- (1)
ŌŚÅ
The negative sign indicates that the quantity of heat lost by liquid goes on
decreasing with time. Where, T = Temperature of the object Ts = Temperature of
the surrounding.
ŌŚÅ
The rate of cooling is high initially and drecreases with falling temperature.
ŌŚÅ
Let us consider an object of mass m and specific heat capacity s at temperature
T. Let Ts be the temperature of the surroundings. If the temperature falls by a
small amount dT in time dt, then the amount of heat lost is,
dQ
= msdT ----------------- (2)
Dividing both sides of equation (2) by
dQ
/ dt = msdT / dt ------------- (3)
ŌŚÅ
From Newton's law of cooling dQ/dt ŌłØ ŌłÆ (TŌłÆTS)
dQ
/ dt = ŌłÆ a (TŌłÆTS) ------------- 4
ŌŚÅ
Where is some positive constant. From equation (3) and (4)
ŌłÆ a (T ŌłÆ Ts) = ms (dt/ dt)
dt
/ (TŌłÆTST) = ŌłÆ (a/ ms) dt ------------- 5
Integrating
equation (5) on both side
╩āŌł×0
[dt / (T - Ts)] = ŌłÆ╩āt0 (a/ms) dt
In
(T ŌłÆ Ts) = ŌłÆ (a/ms)t + b1
ŌŚÅ
Where b1 is the constant of integration, taking exponential on both
sides, we get,
T
= Ts+ b2eŌĆō(a
/ ms) t .
Here
b2 = eb1 = Constant.
8. Explain WienŌĆÖs law and why our eyes are sensitive only to visible rays?
ŌŚÅ
When's law states that, the wavelength of maximum intensity of emission of a
black body radiation is inversely proportional to the absolute temperature of
the black body.
╬╗m
ŌłØ 1/T
or
╬╗m = b / T
 ŌĆ”ŌĆ”ŌĆ”ŌĆ”.. 1
ŌĆ”ŌĆ”ŌĆ”ŌĆ”.. 1
ŌŚÅ
Where, b is known as Wien's constant. Its value is 2.898 ├Ś 10-3 mk
ŌŚÅ
The Sun is approximately taken as a black body.
ŌŚÅ
Since any object above 0 K will emit radiation. Sun also emits radiation.
ŌŚÅ
Its surface temperature is about ; 5700 K. By substituting this value in the
equation (1).
╬╗m
= b / T = 2.858├Ś10-3 / 5700 = 508 nm
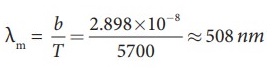
ŌŚÅ
It is the wavelength at which maximium intensity is 508nm.
ŌŚÅ
The visible part of the spectrum lies between 400nm to 700nm.
ŌŚÅ
The humans evolved under the Sun by receiving its radiations. The human eye is
sensitive only in the visible not in infrared or X-ray ranges in the spectrum.

9. Discuss the
a. thermal equilibrium
b. mechanical equilibrium
c. Chemical equilibrium
d. thermodynamic equilibrium.
a.
Thermal equlibrium: Two systems are said to be in thermal equilibrium
with each other if they are at the same temperature, which will not change with
time.
b. Mechanical equilibrium:
ŌŚÅ
Consider a gas container with piston.
ŌŚÅ When some mass is placed on the piston, it move downward due to downward gravitational force and after certain, humps and jumps, the piston will come to rest at a new position.

ŌŚÅ
When the downward gravitational force given by the piston is balanced by the
upward force exerted by the gas, the system is said to be in mechanical
equilibrium.ŌĆā
ŌŚÅ
A system is said to be in mechanical equilibrium if no unbalanced force acts on
the thermo dynamic system or on the surrounding by thermodynamic system.
c.
Chemical equilibrium: If there is no net chemical reaction between two
thermodynamic systems in contact with each other then it is said to be in
chemical equilibrium.
d.
Thermodynamic equilibrium: If two systems are set to be in
thermodynamic equilibrium, then the system are at thermal, mechanical and
chemical equilibrium with each other. In a state of thermodynamic equilibrium
the macroscopic variables such as pressure, volume and temperature will have
fixed values and do not change with time.
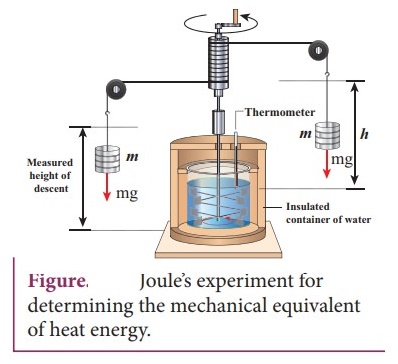
10. Explain JouleŌĆÖs Experiment of the mechanical equivalent of heat.
ŌŚÅ
Joule showed that mechanical energy can be converted into internal energy and
vice versa.
ŌŚÅ
Two masses were attached with a rope and a paddle wheel.
ŌŚÅ
When these masses fall through a distance h hue to gravity, both the masses
lose potential energy equal to 2mgh.
ŌŚÅ
When the masses fall, the paddle wheel turns.
Due
to the turning of wheel inside water, frictional force comes in between the
water and the paddle wheel.
ŌŚÅ
This causes a rise in temperature of the water. This implies that gravitational
potential energy is converted to internal energy of water.
ŌŚÅ
The temperature of water increases due to the work done by the masses.
ŌŚÅ
The mechanical work has the same effect as giving heat.
ŌŚÅ
Joule found that to raise 1 g of an object by 1┬░C, 4.186 J of energy is
required. In earlier days the heat was measured in calorie. 1 cal = 4.186 J.
This is called Joule's mechanical equivalant of heat.
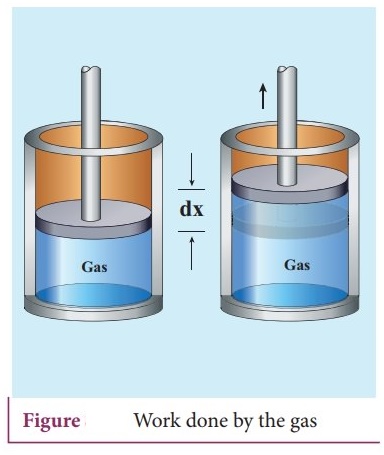
11. Derive the expression for the work done in a volume change in a thermodynamic system.
Work
done in volume changes:
ŌŚÅ
Consider a gas contained in the cylinder fitted with a movable piston. Suppose
the gas is expanded quasi- statically by pushing the piston by a small distance
dx.
ŌŚÅ
Since the expansion occurs quasi-statically the pressure, temperature and
internal energy will have unique values at every instant.
ŌŚÅ
The small work done by the gas on the piston.
dW
= Fdx ŌĆ”ŌĆ”ŌĆ”.. (1)
ŌŚÅ
The force exerted by the gas on the piston F = PA. Here A is area of the piston
and P is pressure exerted by the gas on the piston.
ŌŚÅ
Equation (1) can be rewritten as dW = PA dx ŌĆ”ŌĆ”. (2)
ŌŚÅ
But Adx = dV = change in volume during this expansion process. So the samll
work done by the gas during the expansion is given by dW = PdV ŌĆ”ŌĆ”ŌĆ”. (3)
ŌŚÅ
dV is positive since the volume is increased. So dW is positive.
The
work done by the gas by increasing the volume from Vi to Vf
is given by
W
= Vf╩āVi PdV ŌĆ”ŌĆ”ŌĆ”ŌĆ” (4)
ŌŚÅ
If the work is done on the system, then Vi > Vf. Then,
W is negative. It implies that while the system is doing work, the pressure
need not be constant.
To
evaluate the integration, the pressure is first expressed function of volume
and temperature using the equation of state.
12. Derive MayerŌĆÖs relation for an ideal gas.
Meyer's
relation:
ŌŚÅ
Consider ╬╝ mole of an ideal gas in a container with volume V, pressure P and
temperature T.
ŌŚÅ
When the gas is heated at constant volume the temperature increases by dT. As
no work is done by the gas, the heat that flows into the system will increase
only the internal energy.
ŌŚÅ
Let the change in internal energy be dU.
ŌŚÅ
If Cv is the molar specific heat capacity at constant volume.
dU
= ╬╝Cv dT ŌĆ”ŌĆ”ŌĆ” (1)
ŌŚÅ
Suppose the gas is heated at constant pressure so that the temperature
increases by dT. If 'QŌĆÖ is the head supplied in this process and 'dv' the
change in volume of the gas.
If'
'Q' = ╬╝CP dT ŌĆ”ŌĆ”ŌĆ”. (2)
ŌŚÅ
If W is the work done by the gas in this process, then W = PdV ŌĆ”ŌĆ”ŌĆ”ŌĆ”. (3)
ŌŚÅ
But from the first law of thermodynamics.
Q
= dU + W ŌĆ”.. (4)
ŌŚÅ
Substituting equations (1), (2) and (3) in (4), we get.
╬╝CP dT = ╬╝Cv dT + PdV ŌĆ”ŌĆ”. (5)
ŌŚÅ
For mole of ideal gas, the equation of state is given by PV = ╬╝RT
=>
PdV + VdP = ╬╝RdT ŌĆ”ŌĆ”. (6)
Since
the pressure is constant, dP = 0
CPdT
= CvdT + RdT
CP
= Cv + R (or) CP ŌłÆ Cv = R
This
relation is called Meyer's relation.
13. Explain in detail the isothermal process.
Isothermal
process:
ŌŚÅ
It is a process in which the temperature remains constant but the pressure and
volume of a thermodynamic system will change. The ideal gas equation is
PV
= ╬╝RT, Here, T is constant for this process.
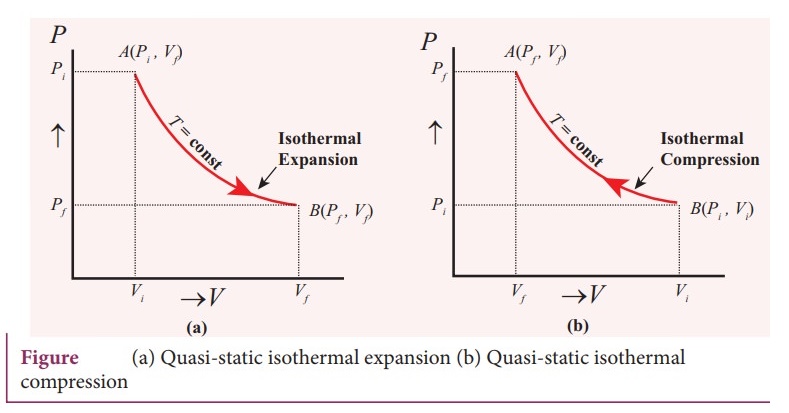
ŌŚÅ
So the equation of state for isothermal process is given by PV = constant ŌĆ”ŌĆ”ŌĆ”..(1)
ŌŚÅ
This implies that if the gas goes from one equilibrium state (P1, V1)
to another equilibrium state (P2, V2) the following
relation holds for this process
P1V1=
P2V2 ŌĆ”ŌĆ”..(2)
ŌŚÅ
Since PV = constant, P is inversely proportional to P ŌłØ 1/V.
ŌŚÅ
This implies that PV graph is a hyperbola. The pressure-volume graph for
constant temperature is also called isotherm.
ŌŚÅ
For an ideal gas the internal energy is a function of temperature only. For an
isothermal process since temperature is constant, the internal energy is also
constant. This implies that dU or ŌłåU = 0.
ŌŚÅ
For an isothermal process, the first law or thermodynamics can be written as
follows,
Q
= W ŌĆ”ŌĆ”ŌĆ”. 3
ŌŚÅ
The heat supplied to a gas used to do only external work.
ŌŚÅ
The isothermal compression takes place when the piston of the cylinder is
pushed. This, will increase the internal energy which will flow out of the
system through thermal contact.
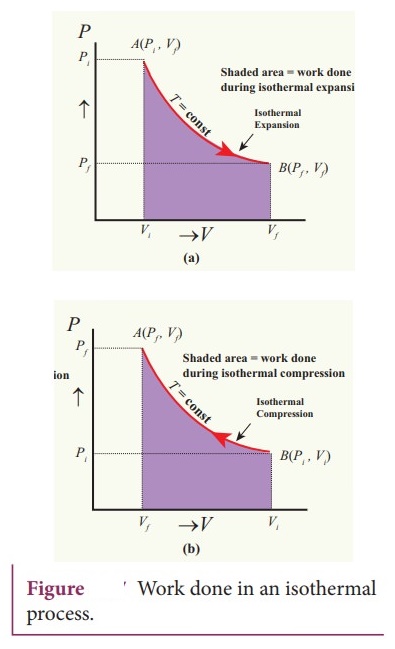
14. Derive the work done in an isothermal process
ŌŚÅ
Consider an ideal gas which is allowed to expand quasi-statically at constant
temperature from initial state (P1, V1) to the final
state (Pf, Vf). The work done by the gas.
W
= Vf╩āVf pdV ------------(1)
ŌŚÅ
As the process occurs quasi-statically, a every stage the gas is at equilibrium
with the surroundings. Since it is in equilibrium at every stage the ideal gas
law is valid.
ŌŚÅ
Writing pressure in terms of volume and temperature.
P
= ╬╝RT / V ----------- (2)
ŌŚÅ
Substituting equation (2) in (1) we get,
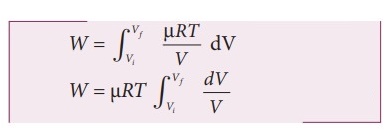
ŌŚÅ
╬╝RT is constant throughout the isothermal process.
ŌŚÅ
By performing the integration in equation (3)
We
get W = ╬╝RT in (Vf / Vi) ----------------- (4)
ŌŚÅ
Since we have an isothermal expansion, Vf /Vi, > 1.
So
In (Vf / Vi) > 0
ŌŚÅ
The work done by the gas during an isothermal expansion is positive.
ŌŚÅ
The above result in equation (4) is true for isothermal compression also. But
in an isothermal compression Vf / Vi < 1. So In (Vf
/ Vi ) < 0. As a result the work done on the gas in an isothermal
compression is negative.
ŌŚÅ
In the PV diagram the work done during the isothermal expansion is equal to the
area under the graph.ŌĆā
ŌŚÅ
For an isothermal compression, the area under the PV graph is equal to the work
done on the gas which turns out to be the area with a negative sign.
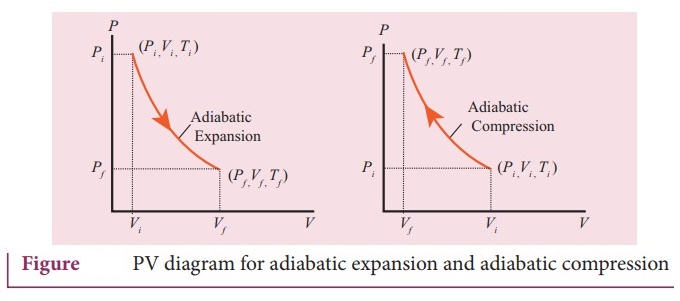
15. Explain in detail an adiabatic process.
Adiabatic process:
ŌŚÅ
This is a process in which no heat flows into or out of the system (Q=0). But
the gas can expand by spending its internal energy or gas can be compressed
through some external work.
ŌŚÅ
So the pressure, volume and temperature of the system may change in an
adiabatic process.
ŌŚÅ
The equation of state for an adiabatic process is given by PV╬│ =
Constant ŌĆ”ŌĆ”ŌĆ” (1).
ŌŚÅ
Here ╬│ is called adiabatic exponent (╬│ = Cp/Cv) which depends on the
nature of the gas.
ŌŚÅ
If the gas goes from an equilibrium state (P1, V1) to
another equilibrium state (Pf, Vf) adiabatically then it
satisfies the relation.
PiVi╬│
= PfVf ╬│ ŌĆ”ŌĆ”ŌĆ”ŌĆ” (2)
ŌŚÅ
The PV diagram for an adiabatic process is also called adiabat.
ŌŚÅ
The PV diagram for isothermal and adiabatic process look similar. But actually
the adiabatic curves is steeper than isothermal curve.
ŌŚÅ
To rewrite the equation (1) in terms of T and V. From ideal gas equation, the
pressure P = ╬╝RT / V. Substituting this equation in the equation (1), we have [
╬╝RT /V ] V╬│ = Constant or [T/V] V╬│ = Constant
/ (╬╝R)
ŌŚÅ
So it can be written as TV╬│ŌłÆ1 = Constant ŌĆ”ŌĆ”. (3)
ŌŚÅ
If the gas goes from an initial equilibrium state (Ti Vi)
to final equilibrium state (Tf Vf) adiabatically then it
satisfies the relation Ti Vi ╬│ŌłÆ1 = Tf
Vf ╬│ŌłÆ1 ŌĆ”ŌĆ”.. (4)
ŌŚÅ The equation of state for adiabatic process can also be written in terms of T and P as T╬│P1-╬│ = Constant ŌĆ”ŌĆ” (5)
16. Derive the work done in an adiabatic process
ŌŚÅ
Consider ╬╝ moles of an ideal gas enclosed in a cylinder having perfectly non
conducting walls and base.
ŌŚÅ A frictionless and insulating piston of cross sectional area A is fitted in the cylinder. Let W be the work done when the system goes from the initial state (Pi, Vi, Ti) to the final state (Pf Vf, Tf) adiabatically, W = Vf╩āViPdV ŌĆ”ŌĆ”ŌĆ”.(1)
ŌŚÅ
The adiabatic process occurs quasi-statically, at every state the ideal gas law
is valid.
ŌŚÅ
Under this conditions the adiabatic equation of state is PV╬│ =
constant (or) P = constant / V╬│ can be substituted in the equation
(1), we get Wadia = Vf╩āVi constant / V╬│ =
dV
=
Constant Vf╩āVi V╬│ dV

But,
= P1V1 = PfVf = constant
Wadia
=1 / (1 ŌĆō ╬│) [ (PfVf ╬│ / Vf╬│
- 1 ) ŌĆō ( PiVi╬│ / Vi╬│
ŌĆō 1) ]
Wadia
= (1 / 1ŌĆō╬│) [PfVf ŌĆō P1V1] ŌĆ”ŌĆ”ŌĆ”ŌĆ”ŌĆ”ŌĆ” 2
From
ideal gas law, PfVf = RTf and P1V1
= ╬╝RT1
Substituting
in equation (2), we get, Wadia = ╬╝R/(╬│ŌĆō1) [TiŌĆōTf]
ŌĆ”ŌĆ”ŌĆ”ŌĆ”ŌĆ”..(3)
ŌŚÅ
In adiabatic expansion, work is done by the gas. i.e., Wadia is
positive. As Ti >Tf, the gas cools during adiabatic
expansion.
ŌŚÅ
In adiabatic compression, work is done on the gas. i.e., Wadia is
negative.
As
Ti >Tf, the temperature of the gas increases during
adiabatic compression.
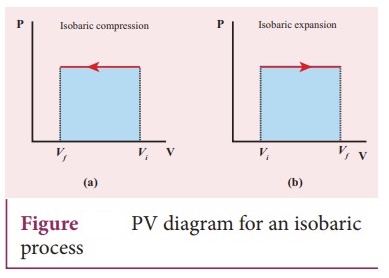
17. Explain the isobaric process and derive the work done in this process
Isobaric
process:
ŌŚÅ
This is a thermodynamic process that occurs at constant pressure. Even though
pressure is constant in this process, temperature, volume and internal energy
are not constant. From the ideal gas equation, we have
V
= [ ╬╝R / P ] T ŌĆ”ŌĆ”ŌĆ”
1
Here ╬╝R / P = Constant

ŌŚÅ
In an isobaric process the temperature is directly proportional to volume.
V
ŌłØ T (Isobaric process) ŌĆ”ŌĆ”ŌĆ”.. (2)
ŌŚÅ
This implies that for a isobaric proces, the V-T graph is a straight line
passing through the origin.
ŌŚÅ
If a gas goes from a state (Vi , Ti) to (Vf, Tf)
at constant pressure, then the system satisfies the following equation
Tf
/ Vf = Ti / Vi
ŌŚÅ
The work done in an isobaric process: Work done by the gas W = vf╩āvi
PdV
ŌŚÅ
In an isobaric process, the pressure is constant W = P vf╩āvi
dV , W = P [Vf ŌłÆ Vi ] = P ╬öV ŌĆ”ŌĆ”ŌĆ”.. (3)
ŌŚÅ
Where ΔV denotes change in the volume. If ΔV is negative, W is also negative.
This implies that the work is done by the gas.
ŌŚÅ
The equation (3) can also be rewritten using the ideal gas equation.
ŌŚÅ
From ideal gas equation PV = ╬╝RT and V = ╬╝RT / P
ŌŚÅ
Substituting this in equation (3) we get, W = ╬╝RTf (1 ŌłÆ Ti/Tf)
ŌŚÅ
In the PV diagram, area under the isobaric curve is equal to the work done in
isobaric process.
ŌŚÅ
The first law of thermodynamics for isobaric process is given by ╬öU = Q ŌłÆ P╬öV.
18. Explain in detail the isochoric process.
Isochoric Process:
This
is a thermodynamic process in which the volume of the system is kept constant.
But
pressure, temperature and internal energy continue to be variables.
The
pressure - volume graph for an isochoric process is a vertical line parallel to
pressure axis.
ŌŚÅ
The equation of state for an isochoric process is given by P = (╬╝R/V)T.
Whrere,
(╬╝R/V)= Constant
ŌŚÅ
The pressure is directly proportional to temperature.
ŌŚÅ
This implies that the P-T graph for an isochoric process is a straight line
passing through origin.
ŌŚÅ
If a gas goes from state (Pi, Ti) to (Pf, Tf)
at constant volume, then the system satisfies the following equation = Pi
/ Ti = Pf / Tf
ŌŚÅ
For an isochoric process, ΔV = 0 and W = 0. Then the first law becomes.
ΔU
= Q
ŌŚÅ
Implying that the heat supplied is used to increase only the internal energy.
Aa
a result the temperature increases and pressure also increases.
ŌŚÅ
Suppose a system loser heat to the surroundings through conducting walls by
keeping the volume constant, then its internal energy decreases.
ŌŚÅ
As a result the temperature decreases; the pressure also decreases.
19. What are the limitations of the first law of thermodynamics?
Limitations
of first law of thermodynamics:
ŌŚÅ
The first law of thermodynamics explains well the inter convertibility of heat
and work.
But
it does not indicate the direction of change.
For
example:
ŌŚÅ
When a hot object is in contact with a cold object, heat always flows from the
hot object to cold object but not in the reverse direction.
ŌŚÅ
According to first law, it is possible for the energy to flow from hot object to
cold object or from cold object to hot object.
ŌŚÅ
The direction of heat flow is always from higher temperature to lower
temperature.
ŌŚÅ
When brakes are applied, a car stops due to friction and the work done against
friction is converted into heat.
ŌŚÅ
But this heat is not reconverted to the kinetic energy of the car.
ŌŚÅ
So the first law is not sufficient to explain many of natural phenomena.ŌĆā
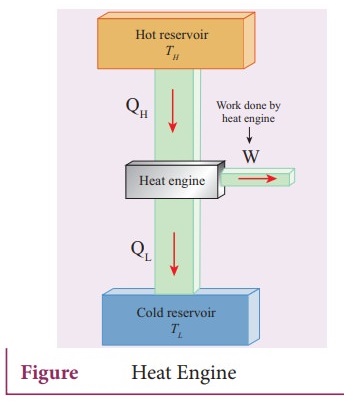
20. Explain the heat engine and obtain its efficiency.
ŌŚÅ
Heat engine is a device which takes heat as input and converts this heat in to
work by undergoing a cyclic process.
A
heat engine has three parts: (a) Hot reservoir, (b) Working
substance, (c) Cold reservoir.
Hot
reservoir (or) source: It supplies heat to the engine. It is always
maintained at a high temperature TH
Working
substance:
ŌŚÅ
It is substance like gas or water, which converts the heat supplied into work.
ŌŚÅ
A simple example of a heat engine is a steam engine. In olden days steam
engines were used to drive trains.
ŌŚÅ
The working substance in these is water which absorbs heat from the burning of
coal.
ŌŚÅ
The heat converts the water into steam.
ŌŚÅ
This steam does work by rotating the wheels of the train, thus making the train
move.
Cold
reservoir (or) Sink: The heat engine ejects some amount of heat (QL)
in to cold reservoir after it doing work. It is always maintained at a low
temperature TL.
ŌŚÅ
For example: In the automobiles engine, the cold reservoir is the
surroundings at room temperature. The automobile ejects heat to these
surroundings through a silencer.
ŌŚÅ
The heat engine works in a cyclic process. After a cyclic process it returns to
the same state.
ŌŚÅ
Since the heat engine returns to the same state after it ejects heat, the
change in the internal energy of the heat engine is zero.
ŌŚÅ The efficiency of the heat engine is defined as the ratio of the work done (output) to the heat absorbed (input) in one cyclic process.

ŌŚÅ
Let the working substance absorb heat QH units from the source and
reject QL units to the sink after doing work W units.
Input
heat = Work done + ejected heat
QH
= W + QL
W
= QH ŌłÆ QL
Then
the efficiency of heat engine ╬Ę = outPut / Input = W/QH = (QHŌłÆ
QL) / QH
╬Ę = Output / Input = W / QH = 1 ŌĆō (QL/QH)
ŌŚÅ
QH, QL and W all are taken as positive, a sign convention
followed in this expression.
Since
QL < QH, the efficiency (╬Ę) always less than 1.
ŌŚÅ
This implies that heat absorbed is not completely converted into work.
ŌŚÅ
The second law of thermodynamics placed fundamental restrictions on converting
heat completely into work.ŌĆā
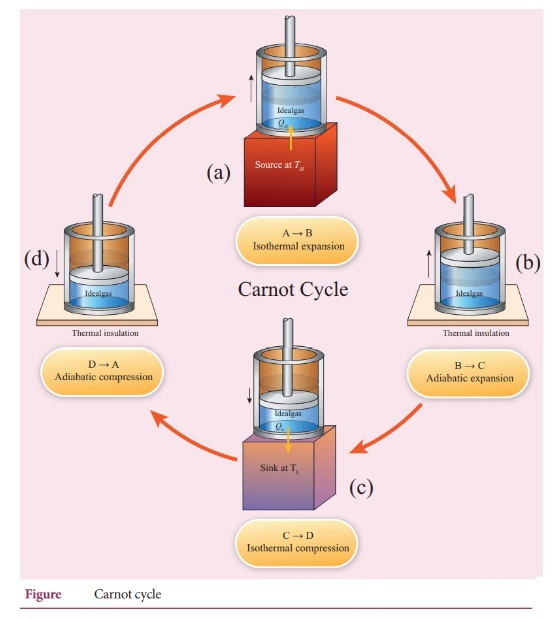
21. Explain in detail Carnot heat engine.
ŌŚÅ
A reversible heat engine operating in a cycle between two temperatures in a
particular way is called a Carnot Engine.
ŌŚÅ
The Carnot engine has four parts which are given below.
Source: It is
the source of heat maintained at constant high temperature TH. Any amount
of heat can be extracted from it, without changing its temperature.
Sink: It is a
cold body maintained at a constant low temperature TL. It can absorb
any amount of heat.
Insulating
stand: It is made of perfectly non-conducting material. Heat is not conducted
through this stand.
Working
substance: It is an ideal gas enclosed in a cylinder with perfectly
non-conducting walls and perfectly conducting bottom. A non-conducting and
frictionless piston is fitted in it.
Carnot's
cycle:
ŌŚÅ
The working substance is subjected to four successive reversible process called
Carnot's cycle.
ŌŚÅ
Let the initial pressure, volume of the working substance be P1 ,V1.
Step
A to B: Quali-static isothermal expansion from (P1,V1,
TH) to (P2, V2, TH).
ŌŚÅ
The cylinder is placed on the source. The heat (QH) flows from
source to the working substance (ideal gas) through the bottom of the cylinder.
Since the process is isothermal, the internal energy of the working substance
will not change.
ŌŚÅ
The input heat increases the volume of the gas. The piston is allowed to move,
out very slowly (quasi-statically).
ŌŚÅ
W1 is the work done by the gas in expanding from volume V1
to volume V2 with a decrease of pressure from P1 to P2.
ŌŚÅ
This is represented by the P-V diagram along the path AB.
ŌŚÅ
Then the work done by the gas (working substance) is given by
QH
= WAŌåÆB = v2╩āv1 PdV
ŌŚÅ
Since the process occurs quasi-statically, the gas is in equlibrium with the
source till it reaches the final state. The work down in the isothermal expansion
is given by the equation.
WAŌåÆB
= ╬╝RTH In ( V2/V1 ) = Area under the curve AB.
Step
B to C: Quasi-static adiabatic expansion from (P2, V2,
TH) to (P3, V3, TH)
ŌŚÅ
The cylinder is placed on the insulating stand and the piston is allowed to
move out.
ŌŚÅ
As the gas expands adiabatically from volume V2 to volume V3
the pressure falls from P2 to P3.
ŌŚÅ
The temperature falls to TL. This adiabatic expansion is represented
by curve BC in the P-V diagram.
ŌŚÅ
This adiabatic process also occurs quasi-statically and implying that this
process is reversible and the ideal gas is in equilibrium throughout the
process.
ŌŚÅ
The work done by the gas in an adiabatic expansion is given by,
WBŌåÆC
= v3╩āv2 PdV = ╬╝R/(╬│ŌłÆ1) [ TH ŌĆō TL] =
Area under the curve BC.
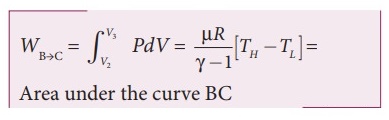
Step
C - D : Quasi-static isothermal compression from (P3, V3,
T1,) to (P4, V4, TL).
ŌŚÅ
The cylinder is placed on the sink and the gas is isothermally compressed until
the pressure and volume become P4 and V4 respectively.
ŌŚÅ
This is represented by the curve CD in the PV diagram.
ŌŚÅ
Let WCŌåÆD be the work done on the gas.
ŌŚÅ
According to first law of thermodynamics.
WCŌåÆD
= v4╩ā v3 PdV = ╬╝RTL In ( V4/V3
) = ŌłÆ ╬╝RTL In ( V3 / V4) = ŌłÆ Area under
curve CD

V3
is greater than V4. So the work done is negative, implying work is
done on the gas.
Step
D-A:
Quasi-static adiabatic compression from (P4, V4, T1)
to (P1, V1, TH).
ŌŚÅ
The cylinder is placed on the insulating stand again and the gas is compressed
adiabatically till it attains the initial pressure P1, volume V1
and temperature TH. This is shown by the curved DA in the P-V
diagram.
WBŌåÆC
v1╩āv4 PdV = -╬╝R / (╬│ ŌłÆ1) [ TL ŌĆō TH]
= Area under the curve DA
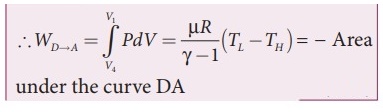
ŌŚÅ
In the adiabatic compression also work is done on the gas so it is negative.
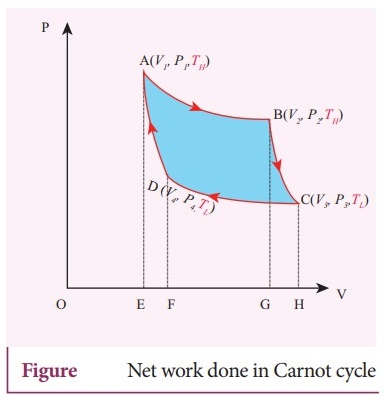
Let 'W' be the net work done by the working substance in one cycle.
Ōł┤WAŌåÆB
+ WBŌåÆC + WCŌåÆD + WDŌåÆA since WDŌåÆA = WBŌåÆC
=
WAŌåÆB + WCŌåÆD
ŌŚÅ
The net work done by the Carnot engine in one cycle W = |W|AŌåÆB ŌłÆ |W|CŌåÆD
ŌŚÅ
The network done by the working substance in one cycle is equal to the area
(enclosed by ABCD) of the P-V diagram.
ŌŚÅ
After, one cycle the working substance returns to the initial temperature TH.
This implies that the change in internal energy of the working substance after
one cycle is zero.
22. Derive the expression for Carnot engine efficiency.
Efficiency
of a Carnot engine:
ŌŚÅ
Efficiency is defined as the ratio of work done by the working substance in one
cycle to the amount of heat extracted from the source.
╬Ę
= Work done / Heat extracted = W/ QH ŌĆ”ŌĆ”..(1)
ŌŚÅ
From the first law of thermodynamics, W = QH ŌłÆ QL
╬Ę
= [ QH - QL ] / QH = 1 [QL / QH] ŌĆ”ŌĆ”ŌĆ”..(2)
ŌŚÅ
Applying isothermal condition, we get,
QH
= ╬╝RTH In (V2 / V1); QL = ╬╝RTL
In (V3 / V4 ) ŌĆ”ŌĆ”ŌĆ”..(3)
ŌŚÅ The amount of (QL) ejected into the sink, (QL/QH ) = [TL In (V3 / V4 ) ] / [ TH In (V2 / V1) ] ŌĆ”ŌĆ”ŌĆ”..(4)
ŌŚÅ
By applying adiabatic conditions, we get, TH V2╬│ŌłÆ1
= TL V3╬│ŌłÆ1
ŌŚÅ
By dividing the above the two equations, we get, (V2 / V1)
╬│ŌłÆ1 = (V3 / V4 ) ╬│ŌłÆ1
ŌŚÅ
Which implies that, V2/V1 = V3/V4 ŌĆ”ŌĆ”ŌĆ”. (5)
ŌŚÅ
Substituting equation (5) in (4), we get, QL/QH = TL/TH
ŌŚÅ
The efficiency ╬Ę = 1 ŌłÆ TL/TH
23. Explain the second law of thermodynamics in terms of entropy.
ŌŚÅ
The quantity QH / TH is equal to QL / QH
the quantity is called entropy.
ŌŚÅ
It is a very important thermodynamic property of system.
ŌŚÅ
It is also state variable QH / TH is the entropy received
by the Carnot engine from hot reservoir and QL/ TL is
entropy given out by the Carnot engine to the cold reservoir.
ŌŚÅ
For reveersible engines (Carnot Engine) both entropies should be same.
ŌŚÅ
So that the change in entropy of the Carnot engine in one cycle is zero. But
for all practical engines like diesel and petrol engines which are not reversible
engines, they satisfy the relation QL/TL > QH/TH
ŌŚÅ
"For all the processes that occur in nature (irreversible process), the
entropy always increases. For reversible process entropy will not change".
ŌŚÅ
Entropy determines the direction in which natural process should occur.
ŌŚÅ
Because entropy increases when heat flows from hot object to cold object. If
heat were to flow from a cold to a hot object.
ŌŚÅ
Entropy will decrease leading to violation of second law thermodynamics.
ŌŚÅ
Entropy is also called 'measure of disorder'. All natural process occur such
that the disorder should always increases.
ŌŚÅ
Consider a bottle with a gas inside. When the gas molecules are inside the
bottle it has less disorder. Once it spreads into the entire room it leads to
more disorder.
ŌŚÅ
In order words when the gas is inside the bottle the entropy is less and once
the gas spreads into entire room, the entropy increases. From the second law of
thermodynamics, entropy always increases.ŌĆā
ŌŚÅ
If the air molecules go back in to the bottle, the entropy should decrease,
which is not allowed by the second law of thermodynamics.
ŌŚÅ
The same explanation applies to a drop of ink diffusing into water. Once the
drop of ink spreads, its entropy is increased.
ŌŚÅ
The diffused ink can never become a drop again. So the natural processes occur
in such a way that entropy should increase for all irreversible process.
24. Explain in detail the working of a refrigerator.
Refrigerator: A
refrigerator is a Carnot's engine working in the reverse order.
Working
principle:
ŌŚÅ
The working substance (gas) absorbs a quantity of heat Q1 from the
cold body (sink) at a lower temperature TL.
ŌŚÅ
A certain amount of work W is done on the working substance by the compressor
and a quantity of heat QH is rejected to the hot body (source) ie.
the atmosphere at TH.
ŌŚÅ
From the first law of thermodynamics.
ŌŚÅ
QL + W = QH AS a
result, the cold reservoir (refrigerator) further cools down and the
surroundings (kitchen or atmosphere) gets hotter.
Co-effeicient
of performance (COP) (╬▓):
ŌŚÅ
Measure of the efficiency of a regrigerator.
ŌŚÅ
The ratio of heat extracted from the cold body (sink) to the enternal work done
by the compressor W.
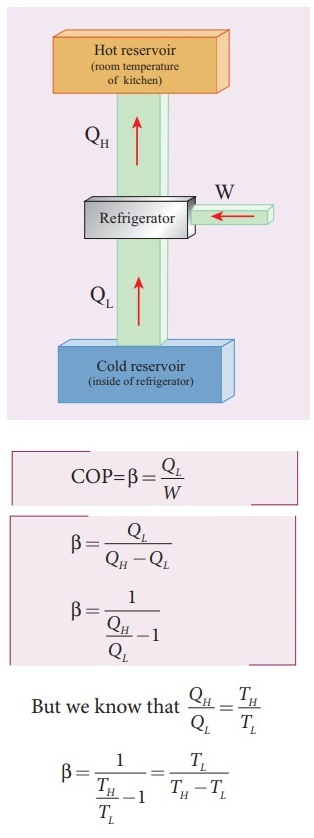
COP
= ╬▓ = QL/W
╬▓
= QL / [QH ŌłÆ QL]
╬▓
= 1 / [ (QH ŌłÆ QL) ŌłÆ 1]
ŌŚÅ
QH / QL = TH / TL
╬▓
= TL / [TH ŌłÆ TL]
ŌŚÅ
Generater the COP, the better is the condition of the refrigerator.
ŌŚÅ
A typical refrigerator has COP around 5 to 6
ŌŚÅ
Lesser the difference in the temperature of the cooling chamber and the
atmosphere, COP is higher.
ŌŚÅ
Without external work heat cannot flow from cold object to hot object.
Related Topics