Isochoric process

Isochoric process

This is a thermodynamic process in which the volume of the system is kept constant. But pressure, temperature and internal energy continue to be variables.

The pressure - volume graph for an isochoric process is a vertical line parallel to pressure axis as shown in Figure 8.37.

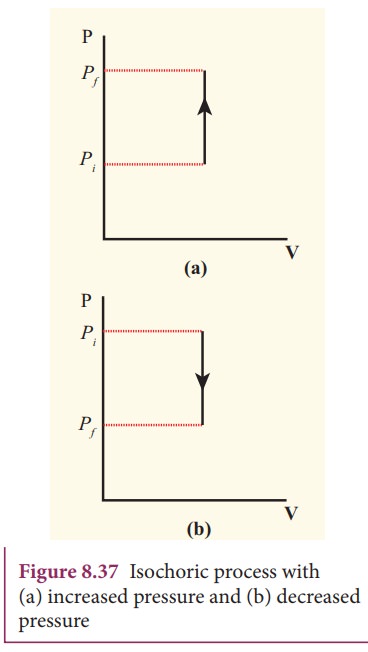
The equation of state for an isochoric process is given by

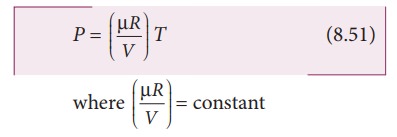
We can infer that the pressure is directly proportional to temperature. This implies that the P-T graph for an isochoric process is a straight line passing through origin.

If a gas goes from state (P_i,T_i) to (P_f,T_f) at constant volume, then the system satisfies the following equation

For an isochoric processes, ∆V=0 and W=0.

Then the first law becomes     

Implying that the heat supplied is used to increase only the internal energy. As a result the temperature increases and pressure also increases. This is shown in Figure 8.38

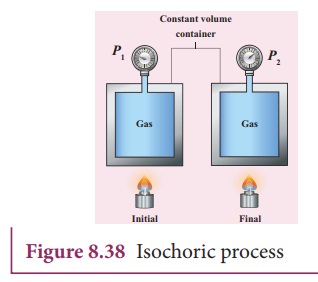
Suppose a system loses heat to the surroundings through conducting walls by keeping the volume constant, then its internal energy decreases. As a result the temperature decreases; the pressure also decreases.

Examples:

1. When food is cooked by closing with a lid as shown in figure.

When food is being cooked in this closed position, after a certain time you can observe the lid is being pushed upwards by the water steam. This is because when the lid is closed, the volume is kept constant. As the heat continuously supplied, the pressure increases and water steam tries to push the lid upwards.

2. In automobiles the petrol engine undergoes four processes. First the piston is adiabatically compressed to some volume as shown in the Figure (a). In the second process (Figure (b)), the volume of the air-fuel mixture is kept constant and heat is being added. As a result the temperature and pressure are increased. This is an isochoric process. For a third stroke (Figure (c)) there will be an adiabatic expansion, and fourth stroke again isochoric process by keeping the piston immoveable (Figure (d)).

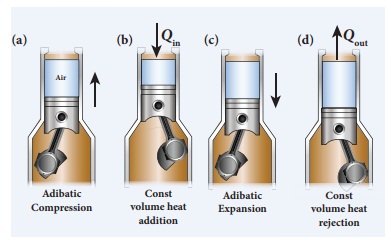
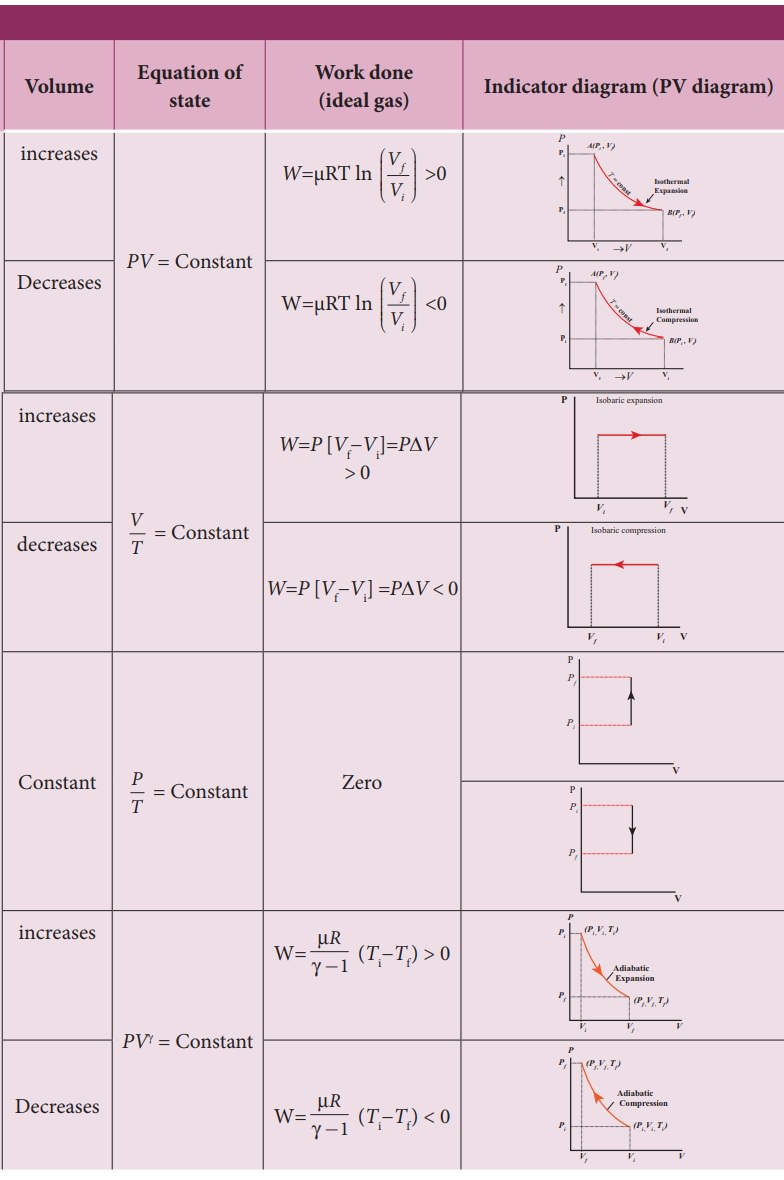
The summary of various thermodynamic processes is give in the Table 8.4.

EXAMPLE 8.21

500 g of water is heated from 30°C to 60°C. Ignoring the slight expansion of water, calculate the change in internal energy of the water? (specific heat of water 4184 J/kg.K)

Solution

When the water is heated from 30°C to 60°C,there is only a slight change in its volume. So we can treat this process as isochoric. In an isochoric process the work done by the system is zero. The given heat supplied is used to increase only the internal energy.

∆U = Q = ms_v ∆T

The mass of water = 500 g =0.5 kg

The change in temperature = 30K

The heat Q = 0.5×4184×30 = 62.76 kJ