Chapter: 11th Physics : UNIT 8 : Heat and Thermodynamics
Solved Example Problems for Boyle’s law, Charles’ law and ideal gas law
EXAMPLE 8.2
A student comes to school by a bicycle whose tire is filled with air at a pressure 240 kPa at 27°C. She travels 8 km to reach the school and the temperature of the bicycle tire increases to 39°C. What is the change in pressure in the tire when the student reaches school?

Solution
We can take air molecules in the tire as an ideal gas. The number of molecules and the volume of tire remain constant. So the air molecules at 27°C satisfies the ideal gas equation P1V1 = NkT1 and at 39°C it satisfies P2V2 = NkT2
But we know
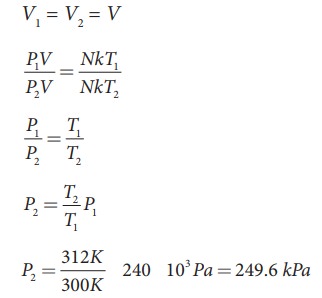
EXAMPLE 8.3
When a person breaths, his lungs can hold up to 5.5 Litre of air at body temperature 37°C and atmospheric pressure (1 atm =101 kPa). This Air contains 21% oxygen. Calculate the number of oxygen molecules in the lungs.
Solution
We can treat the air inside the lungs as an ideal gas. To find the number of molecules, we can use the ideal gas law.
PV = NkT
Here volume is given in the Litre. 1 Litre is volume occupied by a cube of side 10 cm. 1Litre = 10cm √ó 10cm √ó 10cm = 10-3 m3
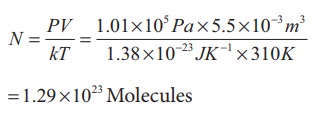
Only 21% of N are oxygen. The total number of oxygen molecules
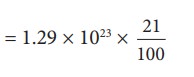
Number of oxygen molecules = 2.7 √ó 1022 molecules
EXAMPLE 8.4
Calculate the volume of one mole of any gas at STP and at room temperature (300K) with the same pressure 1 atm.
Solution:
Here STP means standard temperature (T=273K or 0°C) and Pressure (P=1 atm or 101.3 kPa)
We can use ideal gas equation V = μRT / P.
By substituting the values
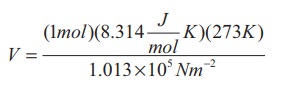
=22.4 √ó 10-3 m3
We know that 1 Litre (L) = =10-3m3. So we can conclude that 1 mole of any ideal gas has volume 22.4 L.
By multiplying 22.4L by 300/273KK we get the volume of one mole of gas at room temperature. It is 24.6 L.
EXAMPLE 8.5
Estimate the mass of air in your class room at NTP. Here NTP implies normal temperature (room temperature) and 1 atmospheric pressure.

Solution
The average size of a class is 6m length, 5 m breadth and 4 m height. The volume of the room V = 6 √ó 5 √ó 4 = 120m3. We can determine the number of mole. At room temperature 300K, the volume of a gas occupied by any gas is equal to 24.6L.
The number of mole μ=
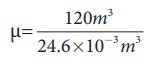
≈4878 mol .
Air is the mixture of about 20% oxygen, 79% nitrogen and remaining one percent are argon, hydrogen, helium, and xenon. The molar mass of air is 29 gmol-1.
So the total mass of air in the room m = 4878 √ó 29 = 141.4kg.
Related Topics