Relation between electric field and potential

Relation between electric field and potential

Consider a positive charge q kept fixed at the origin. To move a unit positive charge by a small distance dx in the electric field E, the work done is given by dW = −E dx. The minus sign implies that work is done against the electric field. This work done is equal to electric potential difference. Therefore,

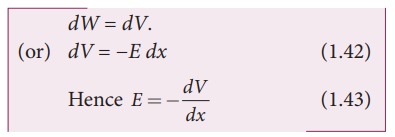
The electric field is the negative gradient of the electric potential. In general,

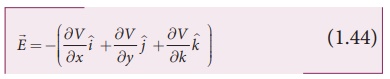
EXAMPLE 1.14

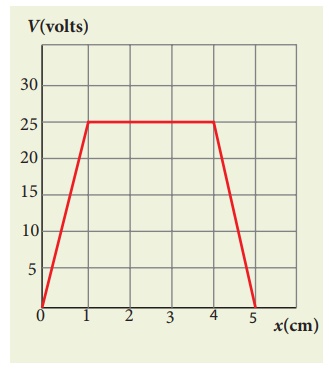
The following figure represents the electric potential as a function of x – coordinate. Plot the corresponding electric field as a function of x.

Solution

In the given problem, since the potential depends only on x, we can use 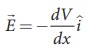(the other two terms ∂V/∂y and ∂V/∂z are zero)

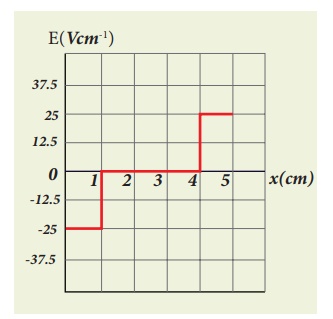
From 0 to 1 cm, the slope is constant and so dV/dx = 25V cm^−1.

So  = −25V cm−1 

From 1 to 4 cm, the potential is constant, V = 25 V. It implies that dV/dx = 0. So  = 0

From 4 to 5 cm, the slope dV/dx = −25V cm^−1.

So  = +25V cm−1 

The plot of electric field for the various points along the x axis is given below.