Applications of Gauss law

Applications of Gauss law

Electric field due to any arbitrary charge configuration can be calculated using Coulomb’s law or Gauss law. If the charge configuration possesses some kind of symmetry, then Gauss law is a very efficient way to calculate the electric field. It is illustrated in the following cases.

(i) Electric field due to an infinitely long charged wire

Consider an infinitely long straight wire having uniform linear charge density λ. Let P be a point located at a perpendicular distance r from the wire (Figure 1.38(a)).

The electric field at the point P can be found using Gauss law. We choose two small charge elements A₁ and A₂ on the wire which are at equal distances from the point P. The resultant electric field due to these two charge elements points radially away from the charged wire and the magnitude of electric field is same at all points on the circle of radius r. This is shown in the Figure 1.38(b). From this property, we can infer that the charged wire possesses a cylindrical symmetry.

Let us choose a cylindrical Gaussian surface of radius r and length L as shown in the Figure 1.39.

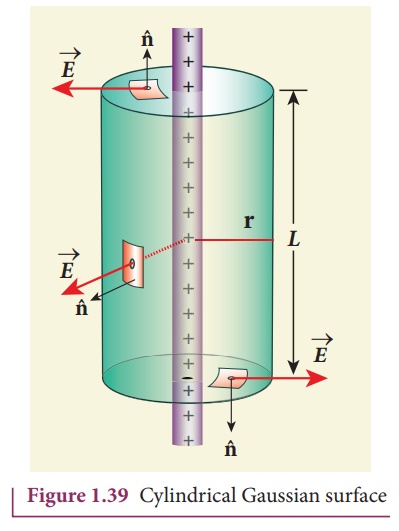
The total electric flux in this closed surface is calculated as follows.

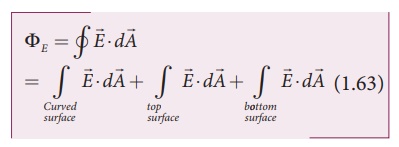
It is seen from Figure (1.39) that for the curved surface,  is parallel to  and  â‹… d  = EdA. For the top and bottom surfaces,  is perpendicular to  and  â‹… d  = 0

Substituting these values in the equation (1.63) and applying Gauss law to the cylindrical surface, we have

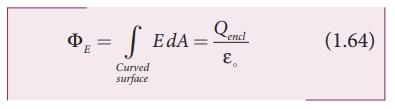
Since the magnitude of the electric field for the entire curved surface is constant, E is taken out of the integration and Q_encl is given by Q_encl = λL .

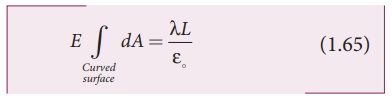
Here 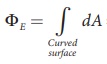 = total area of the curved surface = 2Ï€rL. Substituting this in equation (1.65), we get

The electric field due to the infinite charged wire depends on 1/r rather than 1/r² for a point charge.

Equation (1.67) indicates that the electric field is always along the perpendicular direction ( r^ ) to wire. In fact, if λ > 0 then  points  perpendicular  outward from the wire and if λ < 0, then  points perpendicular inward (-r^).

The equation (1.67) is true only for an infinitely long charged wire. For a charged wire of finite length, the electric field need not be radial at all points. However, equation (1.67) for such a wire is taken approximately true around the mid-point of the wire and far away from the both ends of the wire

(ii) Electric field due to charged infinite plane sheet

Consider an infinite plane sheet of charges with uniform surface charge density σ. Let P be a point at a distance of r from the sheet as shown in the Figure 1.40.

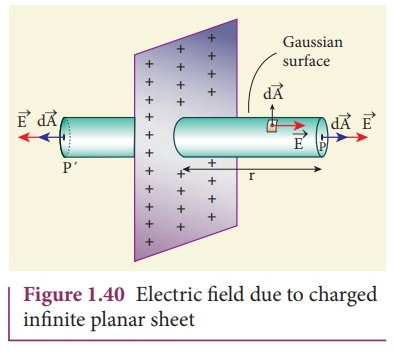
Since the plane is infinitely large, the electric field should be same at all points equidistant from the plane and radially directed at all points. A cylindrical shaped Gaussian surface of length 2r and area A of the flat surfaces is chosen such that the infinite plane sheet passes perpendicularly through the middle part of the Gaussian surface.

Applying Gauss law for this cylindrical surface,

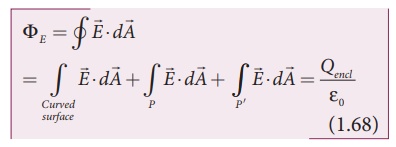
The electric field is perpendicular to the area element at all points on the curved surface and is parallel to the surface areas at P and P′ (Figure 1.40). Then,

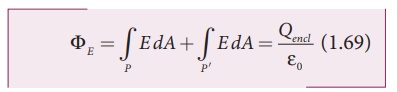
Since the magnitude of the electric field at these two equal surfaces is uniform, E is taken out of the integration and Q_encl is given by Q_encl = σA , we get

Here n^  is the outward unit vector normal to the plane. Note that the electric field due to an infinite plane sheet of charge depends on the surface charge density and is independent of the distance r.

The electric field will be the same at any point farther away from the charged plane. Equation (1.71) implies that if σ > 0 the electric field at any point P is outward perpendicular n to the plane and if σ < 0 the electric field points inward perpendicularly (-n ) to the plane.

For a finite charged plane sheet, equation (1.71) is approximately true only in the middle region of the plane and at points far away from both ends.

(iii) Electric field due to two parallel charged infinite sheets

Consider two infinitely large charged plane sheets with equal and opposite charge densities +σ and -σ which are placed parallel to each other as shown in the Figure 1.41.

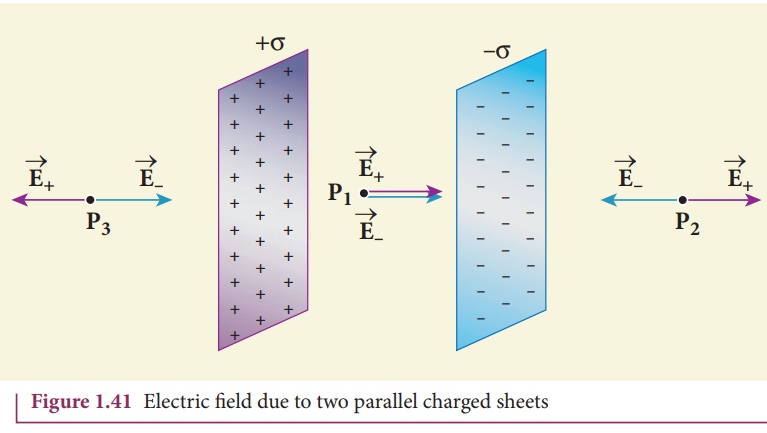
The electric field between the plates and outside the plates is found using Gauss law. The magnitude of the electric field due to

an infinite charged plane sheet is σ/2ε and it points perpendicularly outward if σ > 0 and points inward if σ < 0.

At the points P₂ and P₃, the electric field due to both plates are equal in magnitude and opposite in direction (Figure 1.41). As a result, electric field at a point outside the plates is zero. But inside the plate, electric fields are in same direction i.e., towards the right, the total electric field at a point P₁

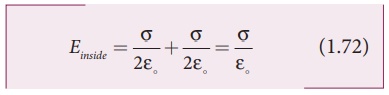
The direction of the electric field inside the plates is directed from positively charged plate to negatively charged plate and is uniform everywhere inside the plate.

(iv) Electric field due to a uniformly charged spherical shell

Consider a uniformly charged spherical shell of radius R and total charge Q as shown in Figure 1.42. The electric field at points outside and inside the sphere is found using Gauss law.

Case (a) At a point outside the shell (r > R) Let us choose a point P outside the shell at a distance r from the center as shown in Figure 1.42 (a). The charge is uniformly distributed on the surface of the sphere (spherical symmetry). Hence the electric field must point radially outward if Q > 0 and point radially inward if Q < 0. So we choose a spherical Gaussian surface of radius r is chosen and the total charge enclosed by this Gaussian surface is Q. Applying Gauss law

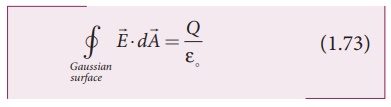
The electric field  and d  point in the same direction (outward normal) at all the points on the Gaussian surface. The magnitude of  is also the same at all points due to the spherical symmetry of the charge distribution.

The electric field is radially outward if Q > 0 and radially inward if Q < 0. From equation (1.75), we infer that the electric field at a point outside the shell will be same as if the entire charge Q is concentrated at the center of the spherical shell. (A similar result is observed in gravitation, for gravitational force due to a spherical shell with mass M)

Case (b): At a point on the surface of the spherical shell (r = R)

The electrical field at points on the spherical shell (r = R) is given by

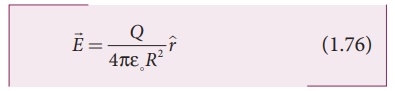
Case (c) At a point inside the spherical shell (r < R)

Consider a point P inside the shell at a distance r from the center. A Gaussian sphere of radius r is constructed as shown in the Figure 1.42 (b). Applying Gauss law

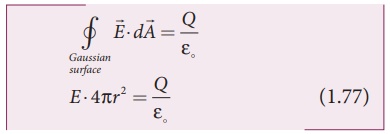
Since Gaussian surface encloses no charge, So Q = 0. The equation (1.77) becomes

The electric field due to the uniformly charged spherical shell is zero at all points inside the shell.

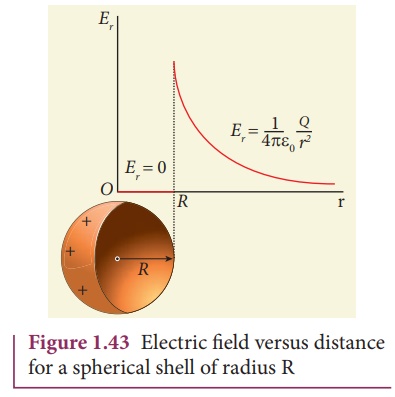
A graph is plotted between the electric field and radial distance. This is shown in Figure 1.43.