Electrostatic Potential energy and Electrostatic potential

ELECTROSTATIC POTENTIAL AND POTENTIAL ENERGY

Introduction

In mechanics, potential energy is defined for conservative forces. Since gravitational force is a conservative force, its gravitational potential energy is defined in XI standard physics (Unit 6). Since Coulomb force is an inverse-square-law force, its also a conservative force like gravitational force. Therefore, we can define potential energy for charge configurations.

Electrostatic Potential energy and Electrostatic potential

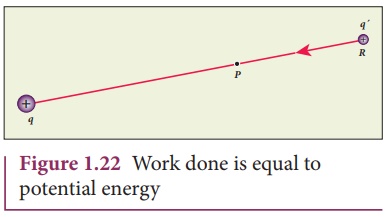
Consider a positive charge q kept fixed at the origin which produces an electric field  around it. A positive test charge q′ is brought from point R to point P against the repulsive force between q and q′ as shown in Figure 1.22. Work must be done to overcome this repulsion. This work done is stored as potential energy.

The test charge q′ is brought from R to P with constant velocity which means that external force used to bring the test charge q′ from R to P must be equal and opposite to the coulomb force 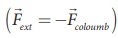. The work done is

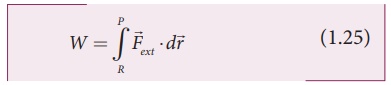
Since coulomb force is conservative, work done is independent of the path and it depends only on the initial and final positions of the test charge. If potential energy associated with q′ at P is U_P and that at R is U_R, then difference in potential energy is defined as the work done to bring a test charge q′ from point R to P and is given as U_P – U_R = W = ΔU

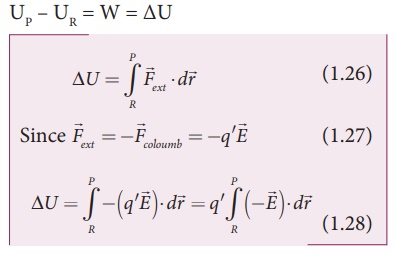
The potential energy difference per unit charge is given by

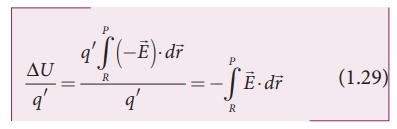
The above equation (1.29) is independent of q′. The quantity 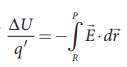is called electric potential difference between P and R and is denoted as V_P – V_R = ∆V.

In otherwords, the electric potential difference is defined as the work done by an external force to bring unit positive charge from point R to point P.

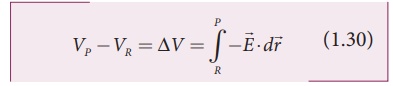
The electric potential energy difference can be written as ∆U = q′ ∆V. Physically potential difference between two points is a meaningful quantity. The value of the potential itself at one point is not meaningful. Therefore the point R is taken at infinity and its potential is considered as zero (V_∞ = 0).

Then the electric potential at a point P is equal to the work done by an external force to bring a unit positive charge with constant velocity from infinity to the point P in the region of the external electric field  .

Mathematically this is written as

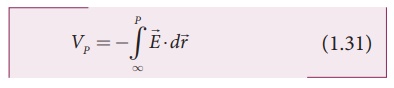
Important points

1. Electric potential at point P depends only on the electric field which is due to the source charge q and not on the test charge q′. Unit positive charge is brought from infinity to the point P with constant velocity because external agency should not impart any kinetic energy to the test charge.

2. From equation (1.29), the unit of electric potential is Joule per coulomb. The practical unit is volt (V) named after Alessandro Volta (1745-1827) who invented the electrical battery. The potential difference between two points is expressed in terms of voltage.