Electrostatic induction

Electrostatic induction

In section 1.1, we have learnt that an object can be charged by rubbing using an appropriate material. Whenever a charged rod is touched by another conductor, charges start to flow from charged rod to the conductor. Is it possible to charge a conductor without any contact? The answer is yes. This type of charging without actual contact is called electrostatic induction.

(i) Consider an uncharged (neutral) conducting sphere at rest on an insulating stand. Suppose a negatively charged rod is brought near the conductor without touching it, as shown in Figure 1.49(a).

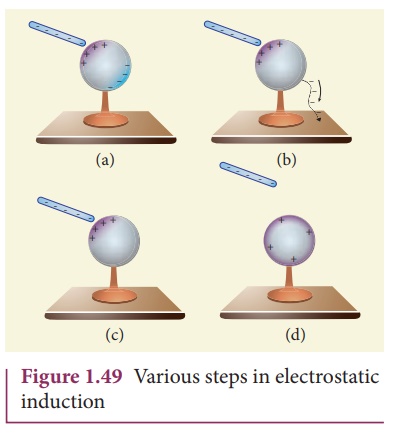
The negative charge of the rod repels the electrons in the conductor to the opposite side. As a result, positive charges are induced near the region of the charged rod while negative charges on the farther side.

Before introducing the charged rod, the free electrons were distributed uniformly on the surface of the conductor and the net charge is zero. Once the charged rod is brought near the conductor, the distribution is no longer uniform with more electrons located on the farther side of the rod and positive charges are located closer to the rod. But the total charge is zero.

(ii) Now the conducting sphere is connected to the ground through a conducting wire. This is called grounding. Since the ground can always receive any amount of electrons, grounding removes the electron from the conducting sphere. Note that positive charges will not flow to the ground because they are attracted by the negative charges of the rod (Figure 1.49(b)).

(iii) When the grounding wire is removed from the conductor, the positive charges remain near the charged rod (Figure 1.49(c))

(iv) Now the charged rod is taken away from the conductor. As soon as the charged rod is removed, the positive charge gets distributed uniformly on the surface of the conductor (Figure 1.49 (d)). By this process, the neutral conducting sphere becomes positively charged.

For an arbitrary shaped conductor, the intermediate steps and conclusion are the same except the final step. The distribution of positive charges is not uniform for arbitrarily-shaped conductors. Why is it not uniform? The reason for it is discussed in the section 1.9

EXAMPLE 1.19

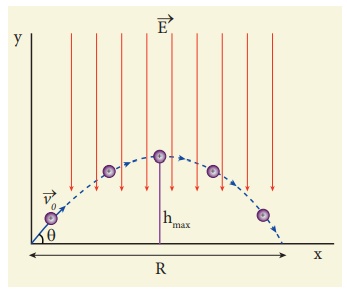
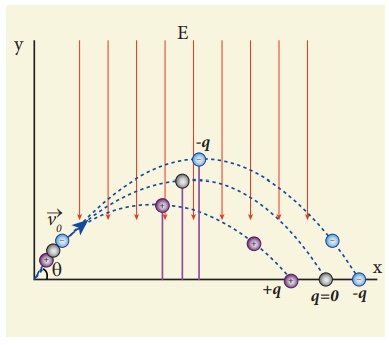
A small ball of conducting material having a charge +q and mass m is thrown upward at an angle θ to horizontal surface with an initial speed v_o as shown in the figure. There exists an uniform electric field E downward along with the gravitational field g. Calculate the range, maximum height and time of flight in the motion of this charged ball. Neglect the effect of air and treat the ball as a point mass.

Solution

If the conductor has no net charge, then its motion is the same as usual projectile motion of a mass m which we studied in Kinematics (unit 2, vol-1 XI physics). Here, in this problem, in addition to downward gravitational force, the charge also will experience a downward uniform electrostatic force.

The acceleration of the charged ball due to gravity = -g j ^

The acceleration of the charged ball due to uniform electric field = -qE/m j ^

The total acceleration of charged ball in downward direction

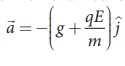
It is important here to note that the acceleration depends on the mass of the object. Galileo’s conclusion that all objects fall at the same rate towards the Earth is true only in a uniform gravitational field. When a uniform electric field is included, the acceleration of a charged object depends on both mass and charge.

But still the acceleration a = ( g + qE/ m ) is constant throughout the motion. Hence we use kinematic equations to calculate the range, maximum height and time of flight.

In fact we can simply replace g by g + qE/m in the usual expressions of range, maximum height and time of flight of a projectile.

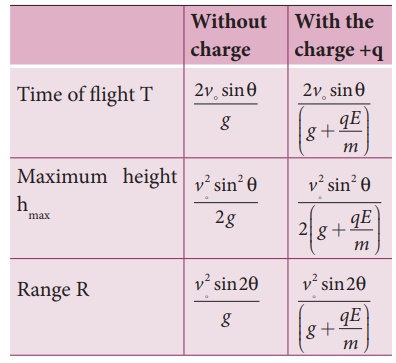
Note that the time of flight, maximum height, range are all inversely proportional to the acceleration of the object. Since ( g + qE/m ) > g for charge +q, the quantities T, h_max, and R will decrease when compared to the motion of an object of mass m and zero net charge. Suppose the charge is –q, then ( g - qE/m ) < g  , and the quantities T, hmax and R will increase. Interestingly the trajectory is still parabolic as shown in the figure.