Chapter: 12th Physics : Electrostatics
Electric field due to continuous charge distribution
Electric field due to continuous charge distribution
The electric charge is
quantized microscopically. The expressions (1.2), (1.3), (1.4) are applicable
to only point charges. While dealing with the electric field due to a charged
sphere or a charged wire etc., it is very difficult to look at individual
charges in these charged bodies. Therefore, it is assumed that charge is
distributed continuously on the charged bodies and the discrete nature of
charges is not considered here. The electric field due to such continuous
charge distributions is found by invoking the method of calculus.![]()
![]()
Consider the following
charged object of irregular shape as shown in Figure 1.9. The entire charged
object is divided into a large number of charge elements ∆q1 , ∆q2 , ∆q 3 ......∆qn and each charge element ∆q is taken as a point
charge.
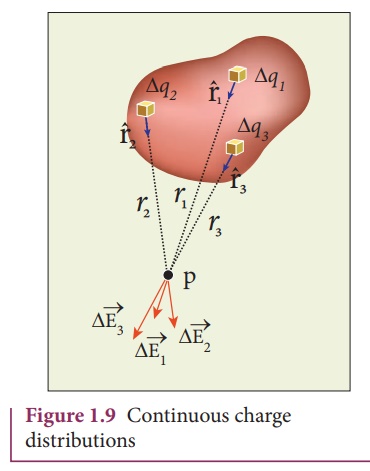
The electric field at a
point P due to a charged object is approximately given by the sum of the fields
at P due to all such charge elements.
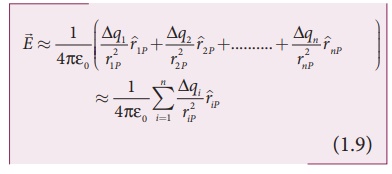
Here ∆qi is the ith
charge element, riP is the distance of the point P from the ith
charge element and ^riP is the unit vector from ith charge
element to the point P.
However the equation
(1.9) is only an approximation. To incorporate the continuous distribution of
charge, we take the limit ∆q → 0 (= dq). In this limit, the
summation in the equation (1.9) becomes an integration and takes the following
form
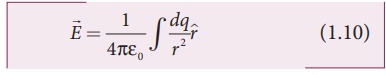
Here r is the distance
of the point P from the infinitesimal charge dq and r is the unit
vector from dq to point P. Even though the electric field for a
continuous charge distribution is difficult to evaluate, the force experienced
by some test charge q in this electric field is still given by 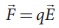 .
.
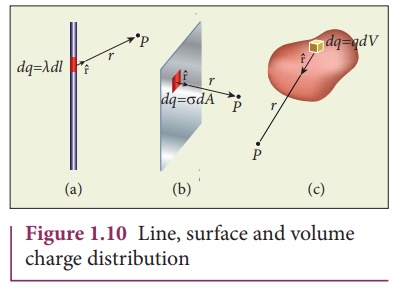
(a) If the charge Q is
uniformly distributed along the wire of length L, then linear charge density
(charge per unit length) is λ
= Q/L . Its
unit is coulomb per meter (Cm-1).
The charge present in
the infinitesimal length dl is dq = λdl. This is shown in
Figure 1.10 (a).
The electric field due
to the line of total charge Q is given by
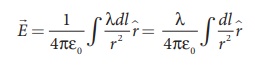
(b) If the charge Q is
uniformly distributed on a surface of area A, then surface charge density
(charge per unit area) is σ
= Q/A . Its
unit is coulomb per square meter (C m-2).
The charge present in
the infinitesimal area dA is dq = σ dA. This is shown in the figure
1.10 (b).
The electric field due
to a of total charge Q is given by
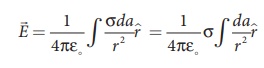
This is shown in Figure
1.10(b).
(c) If the charge Q is
uniformly distributed in a volume V, then volume charge density (charge per
unit volume) is given by ρ
= Q/V . Its
unit is coulomb per cubic meter (C m-3).
The charge present in
the infinitesimal volume element dV is dq = ρdV. This is shown in Figure
1.10(c).
The electric field due
to a volume of total charge Q is given by
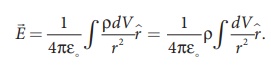
EXAMPLE 1.8
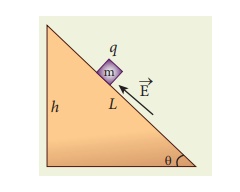
A block of mass m and
positive charge q is placed on an insulated frictionless inclined plane as
shown in the figure. A uniform electric field E is applied parallel to the
inclined surface such that the block is at rest. Calculate the magnitude of the
electric field E.
Solution
Note: A similar problem
is solved in XIth Physics volume I, unit 3 section 3.3.2.
There are three forces
that acts on the mass m:
(i) The downward
gravitational force exerted by the Earth (mg)
(ii) The normal force
exerted by the inclined surface (N)
(iii) The Coulomb force
given by uniform electric field (qE)
The free body diagram
for the mass m is drawn below.

A convenient inertial
coordinate system is located in the inclined surface as shown in the figure.
The mass m has zero net acceleration both in x and y-direction.
Along x-direction,
applying Newton’s second law, we have
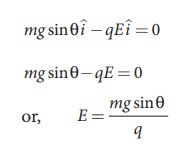
Note that the magnitude
of the electric field is directly proportional to the mass m and inversely proportional
to the charge q. It implies that, if the mass is increased by keeping the
charge constant, then a strong electric field is required to stop the object
from sliding. If the charge is increased by keeping the mass constant, then a
weak electric field is sufficient to stop the mass from sliding down the plane.
The electric field also
can be expressed in terms of height and the length of the inclined surface of
the plane.
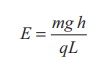
Related Topics