Electrostatics - Coulomb’s Law - Solved Example Problems | 12th Physics : Electrostatics
Chapter: 12th Physics : Electrostatics
Coulomb’s Law - Solved Example Problems
EXAMPLE 1.2
Consider two point charges q1 and q2 at rest as shown in the figure.
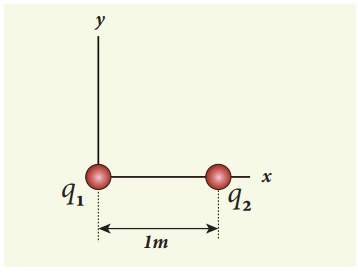
They are separated by a distance of 1m. Calculate the force experienced by the two charges for the following cases:
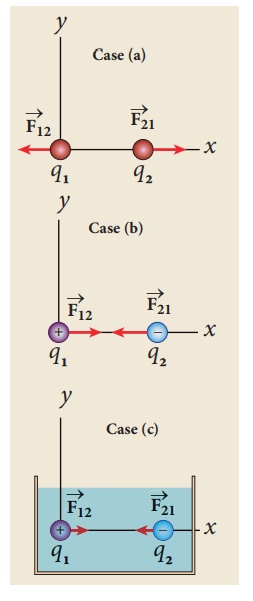
(a) q1 = +2μC and q2 = +3μC
(b) q1 = +2μC and q2 = -3μC
(c) q1= +2μC and q2 = -3μC kept in water (εr = 80)
Solution



EXAMPLE 1.3
Two small-sized identical equally charged spheres, each having mass 1 mg are hanging in equilibrium as shown in the figure. The length of each string is 10 cm and the angle θ is 7° with the vertical. Calculate the magnitude of the charge in each sphere.
(Take g = 10 ms−2)
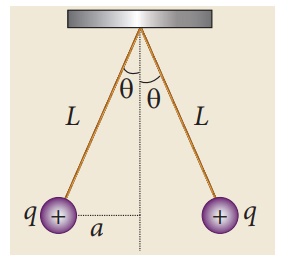
Solution
If the two spheres are neutral, the angle between them will be 0o when hanged vertically. Since they are positively charged spheres, there will be a repulsive force between them and they will be at equilibrium with each other at an angle of 7° with the vertical. At equilibrium, each charge experiences zero net force in each direction. We can draw a free body diagram for one of the charged spheres and apply Newton’s second law for both vertical and horizontal directions.
The free body diagram is shown below.
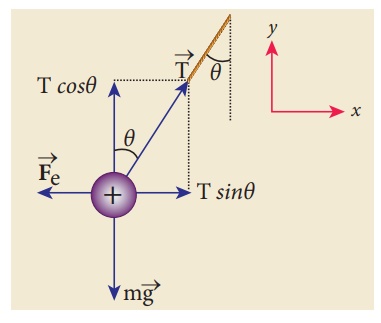
In the x-direction, the acceleration of the charged sphere is zero.
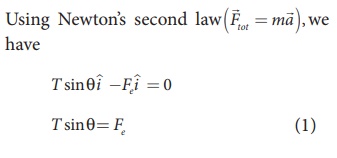
Here T is the tension acting on the charge due to the string and Fe is the electrostatic force between the two charges.
In the y-direction also, the net acceleration experienced by the charge is zero.

EXAMPLE 1.4
Calculate the electrostatic force and gravitational force between the proton and the electron in a hydrogen atom. They are separated by a distance of 5.3 × 10-11 m. The magnitude of charges on the electron and proton are 1.6 × 10-19 C. Mass of the electron is me = 9.1 × 10-31 kg and mass of proton is mp = 1.6 × 10-27 kg.
Solution
The proton and the electron attract each other. The magnitude of the electrostatic force between these two particles is given by
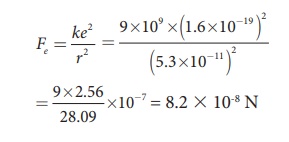
The gravitational force between the proton and the electron is attractive. The magnitude of the gravitational force between these particles is

The electrostatic force between a proton and an electron is enormously greater than the gravitational force between them. Thus the gravitational force is negligible when compared with the electrostatic force in many situations such as for small size objects and in the atomic domain. This is the reason why a charged comb attracts an uncharged piece of paper with greater force even though the piece of paper is attracted downward by the Earth. This is shown in Figure 1.3
EXAMPLE 1.5
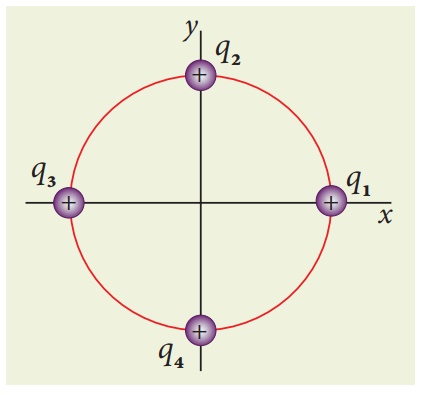
Consider four equal charges q1,q2, q3 and q4 = q = +1μC located at four different points on a circle of radius 1m, as shown in the figure. Calculate the total force acting on the charge q1 due to all the other charges.
Solution
According to the superposition principle, the total electrostatic force on charge q1 is the vector sum of the forces due to the other charges,
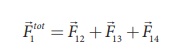
The following diagram shows the direction of each force on the charge q1.
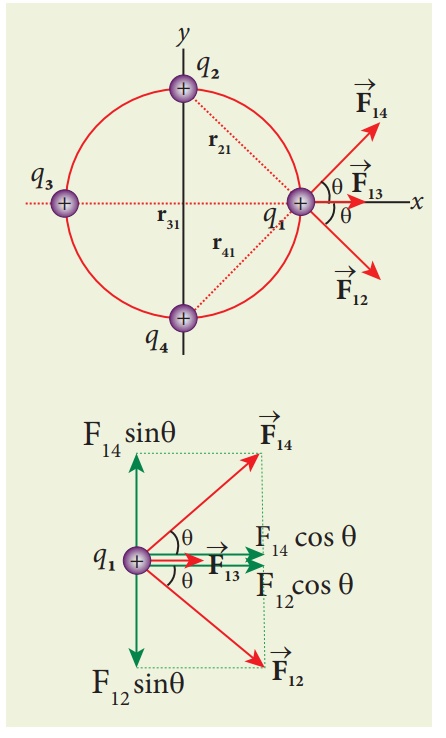
The charges q2 and q4 are equi-distant from q1. As a result the strengths (magnitude) of the forces ![]() and
and ![]() are the same even though their directions are different. Therefore the vectors representing these two forces are drawn with equal lengths. But the charge q3 is located farther compared to q2 and q4. Since the strength of the electrostatic force decreases as distance increases, the strength of the force
are the same even though their directions are different. Therefore the vectors representing these two forces are drawn with equal lengths. But the charge q3 is located farther compared to q2 and q4. Since the strength of the electrostatic force decreases as distance increases, the strength of the force ![]() is lesser than that of forces
is lesser than that of forces ![]() and
and ![]() . Hence the vector representing the force
. Hence the vector representing the force ![]() is drawn with smaller length compared to that for forces
is drawn with smaller length compared to that for forces ![]() and
and ![]() .
.
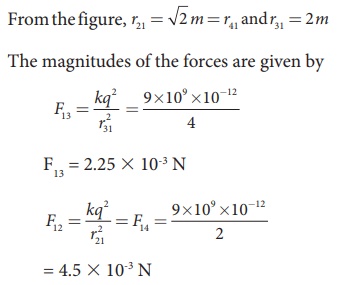
From the figure, the angle θ = 45º. In terms of the components, we have
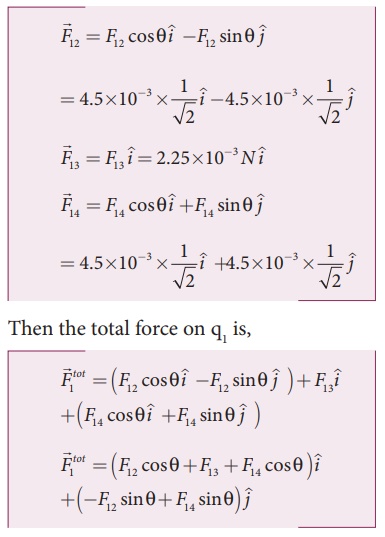
Since F12 = F14, the jth component is zero.
Hence we have
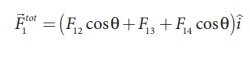
substituting the values in the above equation,
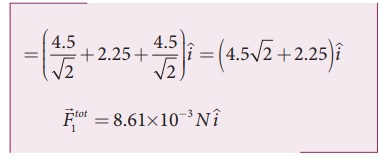
The resultant force is along the positive x axis.
Related Topics