Electrostatic potential at a point due to an electric dipole

Electrostatic potential at a point due to an electric dipole

Consider two equal and opposite charges separated by a small distance 2a as shown in Figure 1.26. The point P is located at a distance r from the midpoint of the dipole. Let θ be the angle between the line OP and dipole axis AB.

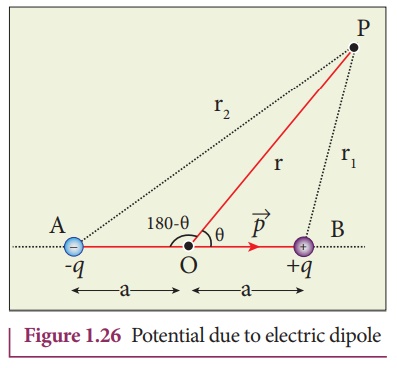
Let r₁ be the distance of point P from +q and r₂ be the distance of point P from –q.

Potential at P due to charge +q  =

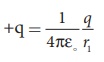
Potential at P due to charge –q=

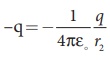
Total potential at the point P,

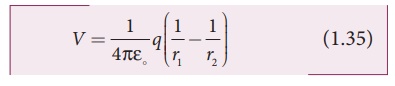
Suppose if the point P is far away from the dipole, such that r>>a, then equation (1.35) can be expressed in terms of r.

By the cosine law for triangle BOP,

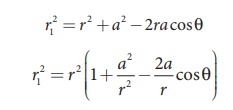
Since the point P is very far from dipole, then r>>a. As a result the term a²/r² is very small and can be neglected. Therefore

Since a/r <<1 , we can use binomial theorem and retain the terms up to first order

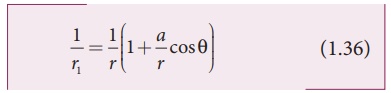
Similarly applying the cosine law for triangle AOP,

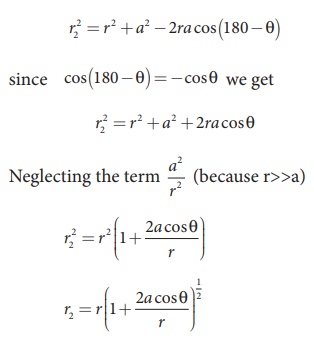
Using Binomial theorem, we get

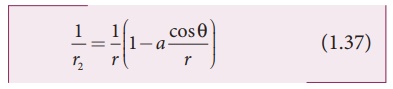
Substituting equation (1.37) and (1.36) in equation (1.35),

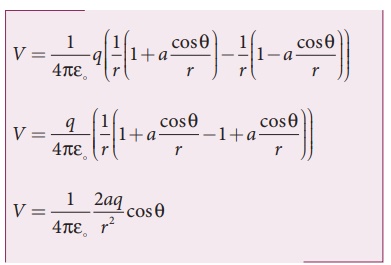
But the electric dipole moment p = 2qa and we get,

Now we can write p cosθ =  Ã—r , where r is the unit vector from the point O to point P. Hence the electric potential at a point P due to an electric dipole is given by

Equation (1.38) is valid for distances very large compared to the size of the dipole. But for a point dipole, the equation (1.38) is valid for any distance.

Special cases

Case (i) If the point P lies on the axial line of the dipole on the side of +q, then θ = 0. Then the electric potential becomes

Case (ii) If the point P lies on the axial line of the dipole on the side of –q, then θ = 180^o, then

Case (iii) If the point P lies on the equatorial line of the dipole, then θ = 90^o. Hence

Important points

(i)  The potential due to an electric dipole Important points falls as 1/r² and the potential due to a single point charge falls as 1/r. Thus the potential due to the dipole^r falls faster than that due to a monopole (point charge). As the distance increases from electric dipole, the effects of positive and negative charges nullify each other.

(ii) The potential due to a point charge is spherically symmetric since it depends only on the distance r. But the potential due to a dipole is not spherically symmetric because the potential depends on the angle between  and position vector  of the point.

However the dipole potential is axially symmetric. If the position vector  is rotated about  by keeping θ fixed, then all points on the cone at the same distance r will have the same potential as shown in Figure 1.27. In this figure, all the points located on the blue curve will have the same potential.