Electrostatic potential energy of a dipole in a uniform electric field

Electrostatic potential energy of a dipole in a uniform electric field

Consider a dipole placed in the uniform electric field  as shown in the Figure 1.31. A dipole experiences a torque when kept in an uniform electric field  . This torque rotates the dipole to align it with the direction of the electric field. 

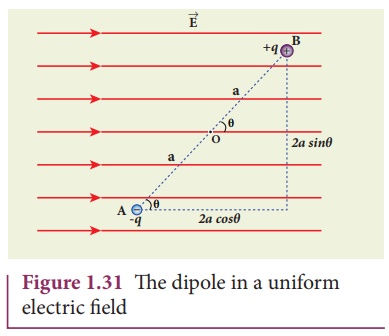
To rotate the dipole (at constant angular velocity) from its initial angle θ’ to another angle θ against the torque exerted by the electric field, an equal and opposite external torque must be applied on the dipole.

The work done by the external torque to rotate the dipole from angle θ’ to θ at constant angular velocity is

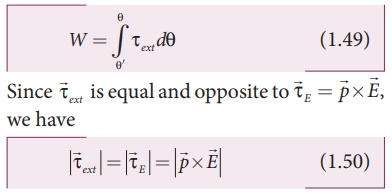
Substituting equation (1.50) in equation (1.49), we get

This work done is equal to the potential energy difference between the angular positions θ and θ′.

U (θ) −U (θ ′)= ∆U = − pE cos θ + pE cosθ′

If the initial angle is θ′ = 90 and is taken as reference point, then U (θ′) = pE cos 90 = 0 .

The potential energy stored in the system of dipole kept in the uniform electric field is given by

In addition to p and E, the potential energy also depends on the orientation θ of the electric dipole with respect to the external electric field.

The potential energy is maximum when the dipole is aligned anti-parallel (θ = π) to the external electric field and minimum when the dipole is aligned parallel (θ = 0) to the external electric field.

EXAMPLE 1.16

A water molecule has an electric dipole moment of 6.3 × 10^-30 Cm. A sample contains 10²² water molecules, with all the dipole moments aligned parallel to the external electric field of magnitude 3 × 10⁵ N C^-1. How much work is required to rotate all the water molecules from θ = 0º to 90º?

Solution

When the water molecules are aligned in the direction of the electric field, it has minimum potential energy. The work done to rotate the dipole from θ = 0º to 90º is equal to the potential energy difference between these two configurations.

W= ∆U =U (90º)−U (0º)

From the equation (1.51), we write U = − pE cosθ, Next we calculate the work done to rotate one water molecule from θ = 0º to 90º.

For one water molecule

W = −pE cos 90º + pE cos0º = pE

W = 6 . 3×10^{− 30} × 3 ×10⁵ = 18 .9×10^−25 J

For 10²² water molecules, the total work done is

W_tot = 18. 9 ×10^{− 25} ×10²² =18 .9×10^−3 J