Brief, Short Answers | Physics - Electrostatics: Questions and Answers | 12th Physics : Electrostatics
Chapter: 12th Physics : Electrostatics
Electrostatics: Questions and Answers
Short Answer Questions
1. What is meant by quantisation of charges?
The charge q on any object is equal to an integral multiple of the fundamental unit of charge e.
q = ne
Here n is any integer (0, ±1, ±2, ±3, ±4……. )
e = 1.6 × l0-19C
2. Write down Coulomb’s law in vector form and mention what each term represents.
Coulomb's law states that the electrostatic force is directly proportional to the product of the magnitude of the point charges and is inversely proportional to the square of the distance between the two point charges.
The force on the point charge q2 exerted by another point charge q1 is
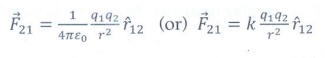
Where ![]() is the unit vector directed from charge q1 to charge q2
is the unit vector directed from charge q1 to charge q2
k is the proportionality constant.
r — distance between the two point charges.
ε0 — Permitivity of free space
3. What are the differences between Coulomb force and gravitational force?
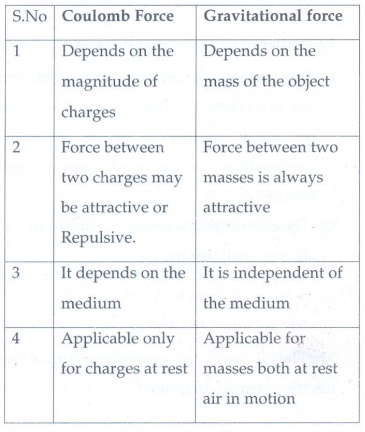
Coulomb Force
1. Depends on the magnitude of charges
2. Force between two charges may be attractive or Repulsive.
3. It depends on the medium
4. Applicable only for charges at rest
Gravitational force
1. Depends on the mass of the object
2. Force between two masses is always attractive
3. It is independent of the medium
4. Applicable for masses both at rest air in motion
4. Write a short note on superposition principle.
According to the superposition principle, the total force acting on a given charge is equal to the vector sum of forces exerted on it by all the other charges.
Consider a system of n charges, q1, q2, q3 .. qn.
The force on q1 exerted by the charge q2.
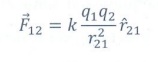
The force on q1 exerted by the charge q3 is
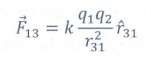
The total force acting on the charge q1 is given by
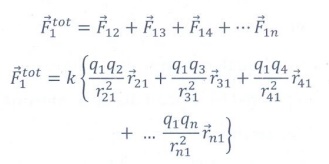
5. Define ‘Electric field’.
The electric field at the point P at a distance r from the point charge q is the force experienced by a unit charge at that point.
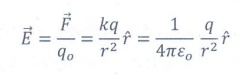
Here ![]() is the unit vector.
is the unit vector.
The electric field is a vector quantity
Its SI unit is NC-1 or Vm-1.
6. What is mean by ‘Electric field lines’?
Electric field lines are an imaginary straight or curved path along which a unit positive charges tends to move in an electric field.
7. The electric field lines never intersect. Justify.
❖ No, two electric field lines intersect each other.
❖ If two lines cross at a point, then there will be two different electric field vectors at the same point.
❖ As a consequence, if some charge is placed in the intersection point then it has to move in two different directions at the same, which is physically impossible. Hence electric field lines do not intersect.
8. Define ‘Electric dipole’
❖ Two equal and opposite charges are separated by a small distance constitute an electric dipole.
❖ Examples: CO, water (H2O), ammonia (NH3), HC1 etc.
❖ The magnitude of electric dipole moment,
![]() = 2qa
= 2qa
Its direction is from - q to +q
9. What is the general definition of electric dipole moment?
❖ The magnitude of the electric dipole moment is equal to the algebraic sum of the product of the magnitude of a charge and the distance of the charge from the origin.
❖ The electric dipole moment for a collection of n point charges is given by
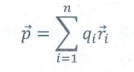
Where ![]() is the position vector of charge qi from the origin.
is the position vector of charge qi from the origin.
10. Define ‘electrostatic potential”.
❖ The electric potential (or) electrostatic potential at a point P is equal to the work done by an external force to bring a unit positive charge with constant velocity from infinity to the point P in the region of the external electric field ![]() .
.
❖ It is a scalar quantity. Its SI unit is volt (V).
11. What is an equipotential surface?
An equipotential surface is a surface on which all the points are at the same potential.
For a point charge the equipotential surfaces are concentric spherical surfaces. For a uniform electric field, it form a set of planes normal to the electric field ![]() .
.
12. What are the properties of an equipotential surface?
Properties of equipotential surfaces
(i) The work done to move a charge q between any two points A and B, W = q (VB - VA). If the points A and B lie on the same equipotential surface, work done is zero because VA = VB.
(ii) The electric field is always normal to an equipotential surface.
13. Give the relation between electric field and electric potential.
The electric field is the negative gradient of the electric potential. In general
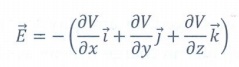
In scalar form E = − dV / dx
14. Define ‘electrostatic potential energy’.
The electric potential at a point at a distance r from point charge q1 is
V = 1/4πεo q1/r
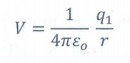
Now if a charge q2 is brought from infinity to that point, a work must be done against the electric field of q1. This workdone is stored as the electrostatic potential energy(U) of a system of charges.
ie U = q2V = 1/4πεo q1q2/r
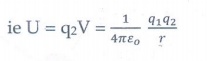
Its unit is Joule. It is a scalar quanity.
15. Define ‘electric flux’
❖ The number of electric field lines crossing a given area kept normal to the electric field lines is called electric flux (ϕ).
❖ It is usually denoted by the Greek letter ΦE and its unit is Nm2C-1 or Vm
❖ Electric flux is a scalar quantity and it can be positive or negative or zero.
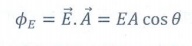
16. What is meant by electrostatic energy density?
The energy stored per unit volume of space is defined as energy density or electrostatic energy density
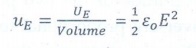
17. Write a short note on ‘electrostatic shielding’.
❖ The process of isolating a certain region of space from external field. It is based on the fact that the electric field inside both hollow and solid conductors is zero.
❖ Eg: Faraday cage.
18. What is Polarisation?
In the presence of an external electric field, the dipole moment is induced in the dielectric material. This is known as dielectric polarisation (or) polarisation.
Polarisation ![]() is defined as the total dipole moment per unit volume of the dielectric.
is defined as the total dipole moment per unit volume of the dielectric.
Polarisation is directly proportional to the strength of the external electric field.
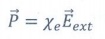
Where χe is a constant called tht electric susceptibility.
19. What is dielectric strength?
❖ When the external electric field applied to a dielectric is very large, it tears the atoms apart so that the bound charges become free charges. Then the dielectric starts to conduct electricity. This is called dielectric breakdown.
❖ The maximum electric field the dielectric can withstand before it breakdowns is called dielectric strength.
❖ The dielectric strength of air is 3 xl06 V/m
20. Define ‘capacitance’. Give its unit.
The capacitance C of a capacitor is defined as the ratio of the magnitude of charge on either of the conductor plates to the potential difference existing between the conductors.
C= Q/V
Its SI unit of capacitance is coulomb per volt or farad (F). Its practical unit is µF or pF
21. What is corona discharge?
The leakage of electric charges from the sharp points of a charged conductor is known as action of points or corona discharge.
III Long Answer questions
1. Discuss the basic properties of electric charges.

Alternative Answer 2:
Basic properties of charges
(i) Electric charge
Most objects in the universe are made up of atoms, which in turn are made up of protons, neutrons and electrons. These particles have mass, an inherent property of particles. Similarly, the electric charge is another intrinsic and fundamental property of particles. The nature of charges is understood through various experiments performed in the 19th and 20th century. The SI unit of charge is coulomb.
(ii) Conservation of charges
Benjamin Franklin argued that when one object is rubbed with another object, charges get transferred from one to the other. Before rubbing, both objects are electrically neutral and rubbing simply transfers the charges from one object to the other. (For example, when a glass rod is rubbed against silk cloth, some negative charge are transferred from glass to silk. As a result, the glass rod is positively charged and silk cloth becomes negatively charged). From these observations, he concluded that charges are neither created or nor destroyed but can only be transferred from one object to other. This is called conservation of total charges and is one of the fundamental conservation laws in physics. It is stated more generally in the following way.
‘The total electric charge in the universe is constant and charge can neither be created nor be destroyed. In any physical process, the net change in charge will always be zero.
(iii) Quantisation of charges
What is the smallest amount of charge that can be found in nature? Experiments show that the charge on an electron is −e and the charge on the proton is +e. Here, e denotes the fundamental unit of charge. The charge q on any object is equal to an integral multiple of this fundamental unit of charge e.

q = ne (1.1)
Here n is any integer (0,±1,±2, ±3, ±4………..). This is called quantisation of electric charge. Robert Millikan in his famous experiment found that the value of e = 1.6 × 10-19C. The charge of an electron is −1.6 × 10-19 C and the charge of the proton is +1.6 × 10-19C.
2. Explain in detail Coulomb’s law and its various aspects.

Alternative Answer 2:
COULOMB’S LAW
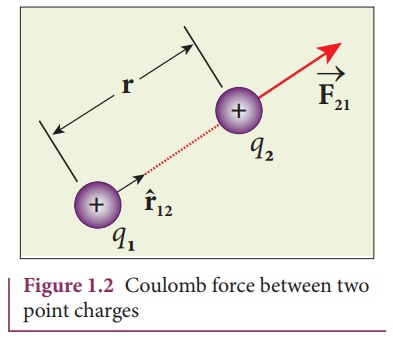
In the year 1786, Coulomb deduced the expression for the force between two stationary point charges in vacuum or free space. Consider two point charges q1 and q2 at rest in vacuum, and separated by a distance of r, as shown in Figure 1.2. According to Coulomb, the force on the point charge q2 exerted by another point charge q1 is
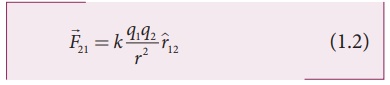
where ^r12 is the unit vector directed from charge q1 to charge q2 and k is the proportionality constant.
Important aspects of Coulomb’s law
(i) Coulomb's law states that the electrostatic force is directly proportional to the product of the magnitude of the two point charges and is inversely proportional to the square of the distance between the two point charges.
(ii) The force on the charge q2 exerted by the charge q1 always lies along the line joining the two charges. ^r12 is the unit vector pointing from charge q1 to q2. It is shown in the Figure 1.2. Likewise, the force on the charge q1 exerted by q2 is along -r^12 (i.e., in the direction opposite to r^12 ).
(iii) In SI units,  and its value is 9 × 109 N m2 C-2. Here ε is the permittivity of free space or vacuum and the value of
and its value is 9 × 109 N m2 C-2. Here ε is the permittivity of free space or vacuum and the value of
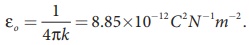
(iv) The magnitude of the electrostatic force between two charges each of one coulomb and separated by a distance of 1 m is calculated as follows:
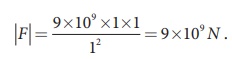
This is a huge quantity, almost equivalent to the weight of one million ton. We never come across 1 coulomb of charge in practice. Most of the electrical phenomena in day-to-day life involve electrical charges of the order of µC (micro coulomb) or nC (nano coulomb).
(v) In SI units, Coulomb’s law in vacuum takes the form 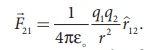 In a medium of permittivity ε, the force between two point charges is given by
In a medium of permittivity ε, the force between two point charges is given by 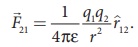
Since ε>εo , the force between two point charges in a medium other than vacuum is always less than that in vacuum. We define the relative permittivity for a given medium as εr>ε/εo . For vacuum or air, εr = 1 and ε for all other media εr> 1.![]()
(vi) Coulomb’s law has same structure as Newton’s law of gravitation. Both are inversely proportional to the square of the distance between the particles. The electrostatic force is directly proportional to the product of the magnitude of two point charges and gravitational force is directly proportional to the product of two masses. But there are some important differences between these two laws.
· The gravitational force between two masses is always attractive but Coulomb force between two charges can be attractive or repulsive, depending on the nature of charges.
· The value of the gravitational constant G = 6.626 × 10-11 N m2 kg-2. The value of the constant k in Coulomb law is k = 9 × 109 N m2 C-2. Since k is much more greater than G, the electrostatic force is always greater in magnitude than gravitational force for smaller size objects.
· The gravitational force between two masses is independent of the medium. For example, if 1 kg of two masses are kept in air or inside water, the gravitational force between two masses remains the same. But the electrostatic force between the two charges depends on nature of the medium in which the two charges are kept at rest.
· The gravitational force between two point masses is the same whether two masses are at rest or in motion. If the charges are in motion, yet another force (Lorentz force) comes into play in addition to coulomb force.
(vii) The force on a charge q1 exerted by a point charge q2 is given by
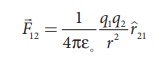
Here ^r21 is the unit vector from charge q2 to q1.
But ^r21 = − ^r12 ,
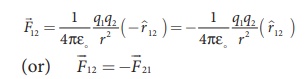
Therefore, the electrostatic force obeys Newton’s third law.
(viii) The expression for Coulomb force is true only for point charges. But the point charge is an ideal concept. However we can apply Coulomb’s law for two charged objects whose sizes are very much smaller than the distance between them. In fact, Coulomb discovered his law by considering the charged spheres in the torsion balance as point charges. The distance between the two charged spheres is much greater than the radii of the spheres.
3. Define ‘Electric field’ and discuss its various aspects.

4. Calculate the electric field due to a dipole on its axial line and equatorial plane.


5. Derive an expression for the torque experienced by a dipole due to a uniform electric field.

6. Derive an expression for electrostatic potential due to a point charge.

7. Derive an expression for electrostatic potential due to an electric dipole.

8. Obtain an expression for potential energy due to a collection of three point charges which are separated by finite distances.

9. Derive an expression for electrostatic potential energy of the dipole in a uniform electric field.

10. Obtain Gauss law from Coulomb’s law.

11. Obtain the expression for electric field due to an infinitely long charged wire.

12. Obtain the expression for electric field due to an charged infinite plane sheet.

13. Obtain the expression for electric field due to an uniformly charged spherical shell.

14. Discuss the various properties of conductors in electrostatic equilibrium.

15. Explain the process of electrostatic induction.

16. Explain dielectrics in detail and how an electric field is induced inside a dielectric.

17. Obtain the expression for capacitance for a parallel plate capacitor.

18. Obtain the expression for energy stored in the parallel plate capacitor.

19. Explain in detail the effect of a dielectric placed in a parallel plate capacitor.

20. Derive the expression for resultant capacitance, when capacitors are connected in series and in parallel.

21. Explain in detail how charges are distributed in a conductor, and the principle behind the lightning conductor.

22. Explain in detail the construction and working of a Van de Graaff generator.

Related Topics