Capacitance of a parallel plate capacitor

Capacitance of a parallel plate capacitor

Consider a capacitor with two parallel plates each of cross-sectional area A and separated by a distance d as shown in Figure 1.56.

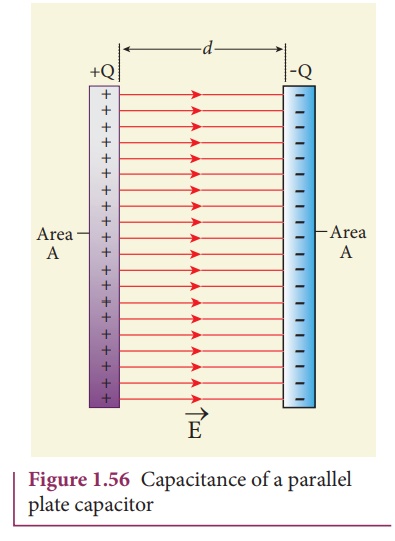
The electric field between two infinite parallel plates is uniform and is given by E = σ / ε0 where σ is the surface charge density on the plates  (σ=Q/A) If the separation distance d is very much smaller than the size of the plate (d2 << A), then the above result is used even for finite–sized parallel plate capacitor.

The electric field between the plates is

Since the electric field is uniform, the electric potential between the plates having separation d is given by

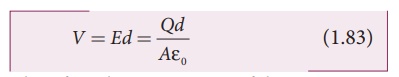
Therefore the capacitance of the capacitor is given by

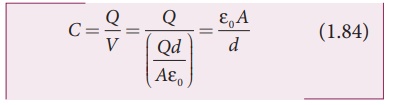
From equation (1.84), it is evident that capacitance is directly proportional to the area of cross section and is inversely proportional to the distance between the plates. This can be understood from the following.

(i) If the area of cross-section of the capacitor plates is increased, more charges can be distributed for the same potential difference. As a result, the capacitance is increased.

(ii) If the distance d between the two plates is reduced, the potential difference between the plates (V = Ed) decreases with E constant. As a result, voltage difference between the terminals of the battery increases which in turn leads to an additional flow of charge to the plates from the battery, till the voltage on the capacitor equals to the battery’s terminal voltage. Suppose the distance is increased, the capacitor voltage increases and becomes greater than the battery voltage. Then, the charges flow from capacitor plates to battery till both voltages becomes equal.

Example 1.20

A parallel plate capacitor has square plates of side 5 cm and separated by a distance of 1 mm. (a) Calculate the capacitance of this capacitor. (b) If a 10 V battery is connected to the capacitor, what is the charge stored in any one of the plates? (The value of εo = 8.85 x 10-12 Nm2 C-2)

Solution

(a) The capacitance of the capacitor is

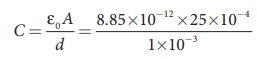
= 221.2 ×10−13 F

C = 22 . 12 ×10−12 F = 22 .12 pF

(b) The charge stored in any one of the plates is Q = CV, Then

= 22 . 12 ×10−12 Ã—10 = 221.2 ×10−12 C = 221.2 pC